Обобщенные координаты, принцип возможных перемещений, обобщенные силы, страница 2

            1. Системе необходимо сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не изменяются.

            На этом перемещении подсчитывается элементарная работа активных сил и то, что будет коэффициентом при  и будет обобщенной силой , соответствующей обобщенной координате . Затем системе сообщается перемещение, при котором изменяется только координата , и аналогичным образом находится сила  и так далее.

            2. Записывается выражение для потенциальной энергии системы как функция обобщенных координат:

;

            Тогда обобщенные силы находятся как взятые с обратным знаком частные производные от потенциальной энергии по обобщенным координатам:

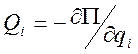
            Этот метод более удобен в тех случаях, когда все силы системы являются потенциальными.

Пример 1.

Два груза с массами m1 и m2 соединены невесомой нитью, переброшенной через невесомый блок без трения в оси. Грузы могут двигаться только в вертикальном направлении. Найти обобщенную силу системы.     У данной системы одна степень свободы и в качестве обобщенной координаты выберем координату q, определяющую положение груза m2. Изобразим действующие на систему силы и сообщим системе возможное перемещение dq.

Вычислим элементарную работу сил на этом перемещении:

;

            Коэффициент при dq и есть обобщенная сила системы:

;

       Запишем зависимость потенциальной энергии системы от обобщенной координаты q:

;

            В этом выражении знаки слагаемых можно пояснить так: с ростом координаты q груз 2 опускается и его потенциальная энергия убывает, а груз 1 поднимается и его потенциальная энергия возрастает.

            Используя второй метод определения обобщенной силы получим такое же выражение для обобщенной силы:

;

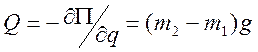Пример 2.

Три груза с весами P1=m1g, P2=m2g и P3=m3g с помощью двух невесомых блоков без трения и двух нитей объединены в механическую систему. Грузы могут двигаться только в вертикальном направлении. Найти обобщенные силы системы.  У данной системы две степени свободы и в качестве двух обобщенных координат выберем координаты q1 (положение груза 1) и q2 (положение груза 3).

            Сообщим системе такое возможное перемещение dq₁ , при котором будет меняться координата q₁, а другая координата будет фиксированной (фиксируем груз 3 и даем возможность грузу 1 совершить перемещение dq₁, при этом груз 2 поднимется на величину 2dq₁). Вычислим элементарную работу на этом перемещении:

;

            Таким образом, первая обобщенная сила будет иметь вид: .

            Сообщим теперь системе такое возможное перемещение dq₂ , при котором будет меняться только координата q₂, а другая координата q₁ будет фиксированной (фиксируем груз 1 и даем возможность грузу 3 совершить перемещение dq₂, при этом груз 2 поднимется вверх на величину dq₂). Вычислим элементарную работу на этом перемещении:

;

            Для второй обобщенной силы получаем выражение:  .

            Определим эти обобщенные силы вторым способом (через потенциальную энергию). Потенциальная энергия системы будет следующим образом зависеть от обобщенных координат:

;

            Здесь с ростом координат q₁ и q₂ потенциальная энергия грузов 1 и 3 уменьшается, а груза 2 – увеличивается (с ростом q₁ и q₂ груз 2 поднимается на величину q₂ + 2q₁). Взяв частные производные от потенциальной энергии по обобщенным координатам найдем: