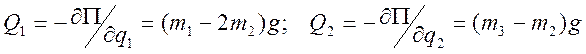
Пример 3.
|
|
Левый конец вала зафиксирован в стенке (жесткая заделка), правый конец может свободно вращаться в подшипнике. С валом жестко скреплены три диска. Диски могут совершать поворот относительно оси вала, то есть участки вала испытывают упругую деформацию закручивания (коэффициент жесткости вала на упругое закручивание – с). Определить обобщенные силы системы. |
Система имеет три степени свободы. В качестве обобщенных координат выберем углы поворота дисков относительно оси вала j1, j2 и j3 (диски совершают повороты относительно оси, лежащей в плоскости рисунка). Если диски повернутся на углы j1, j2 и j3, то участок вала I будет закручен на угол j1, участок вала II – на угол j2 - j1, участок вала III – на угол j3 - j2. Участок вала IV закручен не будет, так как правый конец вала свободно вращается в подшипнике. Потенциальная энергия системы сосредоточена в упруго-закрученных участках вала I, II, III и описывается следующим выражением:
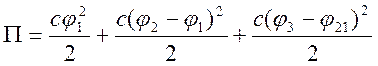 ;
;
Получим обобщенные силы системы:
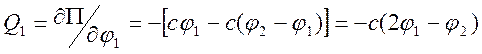 ;
;
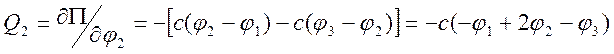 ;
;
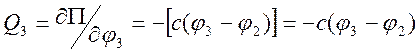 ;
;
Пример 4.
|
|
На цилиндр радиуса a намотана нить, к свободному концу которой прикреплен точечный груз массы m. Длина нити в состоянии равновесия системы равна l. Груз может совершать колебательное движение в плоскости рисунка. Определить обобщенную силу системы. Система имеет одну степень свободы. В качестве обобщенной координаты выберем угол q (угол отклонения нити от вертикали). Потенциальная энергия груза определяется выражением: |
![]()
Тогда обобщенная сила будет иметь вид:
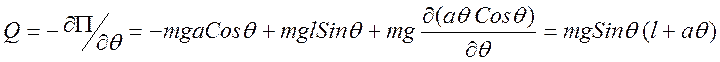
§3.18 Уравнения Лагранжа 2-го рода
Предположим теперь, что для движения точки по линии (см. §3.16) уравнения связей f1(x,y,z)=0 и f2(x,y,z)=0 удовлетворяются тождественно по отношению к t и q (обобщенная криволинейная координата – длина дуги, пройденного точкой по линии) соотношениями:
x=x(q,t), y=y(q,t), z=z(q,t); (3.18.1)
На эти уравнения можно смотреть как на параметрическое представление уравнений связей, наложенных на точку. Дифференцируя при этом предположении уравнения связей f1(x,y,z)=0 и f2(x,y,z)=0 по параметру q, будем иметь:
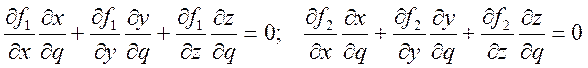 ; (3.18.2)
; (3.18.2)
Умножая
(3.16.1) соответственно на 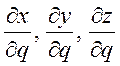 и складывая, будем
иметь в силу (3.18.2):
и складывая, будем
иметь в силу (3.18.2):
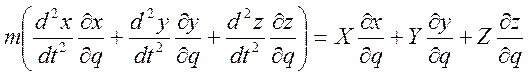 ; (3.18.3)
; (3.18.3)
Правая часть этого выражения – определенная в §3.17 (ф.3.17.1) обобщенная сила. Наша задача заключается в преобразовании левой части (3.18.3) с целью полностью перейти к обобщенной координате q.
Рассмотрим производную по времени от координаты x имея в виду, что она в соответствии с (3.18.1) является функцией q:
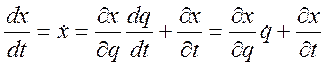 ; (3.18.4)
; (3.18.4)
Взяв
от (3.18.4) частную производную по ![]() найдем:
найдем:
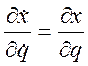 ; (3.18.5)
; (3.18.5)
Также, взяв частную производную от (3.18.4) по независимой обобщенной координате q найдем:
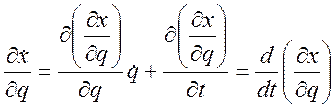 , то
есть
, то
есть
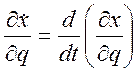 ; (3.18.6)
; (3.18.6)
Соотношения, аналогичные (3.18.5) и (3.18.6), можно, очевидно, также получить для координат y и z.
Левую часть выражения (3.18.3) можно представить в виде:
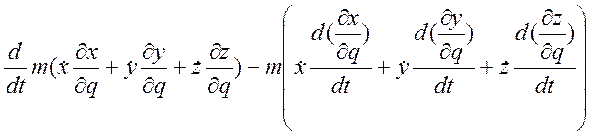 ;
;
Здесь
применена формула для дифференцирования произведения функций: ![]() .
Используя теперь (3.18.5) и (3.18.6) этот результат можно переписать в виде:
.
Используя теперь (3.18.5) и (3.18.6) этот результат можно переписать в виде:
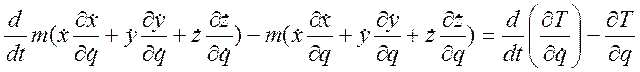 ;
;
где
T обозначает кинетическую энергию точки 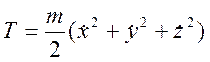 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.