Окончательно получаем уравнение движения точки в обобщенной координате или уравнение Лагранжа 2-го рода:
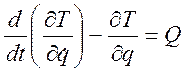 ;
;
Уравнения
Лагранжа 2-го рода примечательны тем, что для их записи достаточно знать
выражение кинетической энергии как функции ![]() и
обобщенную силу.
и
обобщенную силу.
Если
обобщенную силу можно представить через обобщенную потенциальную энергию P(q): 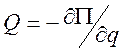 , то уравнение Лагранжа
примет вид:
, то уравнение Лагранжа
примет вид:
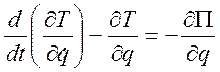 или
или 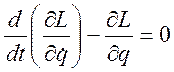 , где
, где ![]() называется
функцией Лагранжа.
называется
функцией Лагранжа.
Рассмотрим более общий случай:
x=x(q, q2, q3, t); y=y(q, q2, q3, t); z=z(q, q2, q3, t); (3.18.7)
где qa (a=1…k, k=1 или k=2 или k=3). Уравнения (3.8.17) выражают связи, наложенные на точку. Если k=1, то мы имеем случай, когда материальная точка стеснена условиями находиться на линии (имеет одну степень свободы и одну обобщенную координату). Если k=2 (a=1,2), то точка стеснена условием находиться на поверхности и имеет две степени свободы и две обобщенные координаты. В случае k=3 (3.18.7) будет выражать переход от декартовых координат x,y,z к некоторым криволинейным координатам q, q2, q3.
При движении точки по поверхности имеем для нее две степени свободы. С помощью аналогичных предыдущему случаю (движение точки по линии) выкладок можно получить:
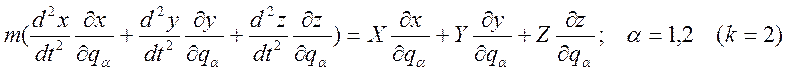 ;
;
Повторяя преобразования, подобные сделанным ранее, получим:
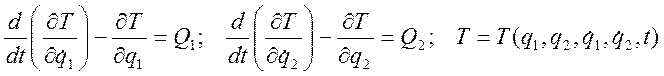
Для свободно точки и криволинейных координат будем иметь:
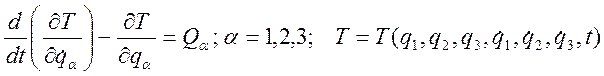 ;
;
Для механической системы с m степенями свободы (такая система описывается с помощью m обобщенных координат) имеем уравнения Лагранжа 2-го рода:
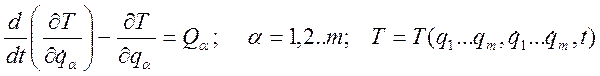 ;
;
Число уравнений равно числу степеней свободы системы, это минимально необходимое число уравнений, которые необходимо составить для описания движения системы. Для записи уравнений Лагранжа нужно записать выражение кинетической энергии системы как функции обобщенных координат, обобщенных скоростей, времени и найти обобщенные силы системы. После этого процесс получения системы уравнений сводится к техническим операциям по дифференцированию. В конечном итоге мы получим систему обыкновенных дифференциальных уравнений второго порядка в числе, равном числу степеней свободы механической системы. Если будут заданы начальные условия, то после интегрирования этой системы уравнений будет получен закон движения механической системы, то есть зависимости обобщенных координат от времени.
Продемонстрируем использование формализма уравнений Лагранжа на примерах из §17 и составим уравнения движения:
Пример 1.
|
|
Выражение для кинетической энергии данной системы имеет вид:
Получаем уравнение Лагранжа, описывающее движение системы:
|
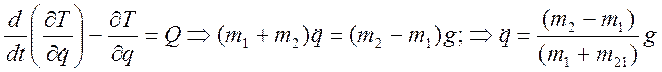 ;
;
Пример 2.
|
|
Выражение для кинетической энергии данной системы имеет вид:
Получаем систему двух уравнений Лагранжа:
|
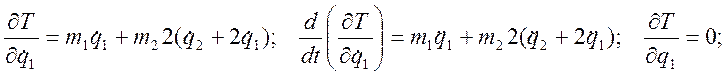
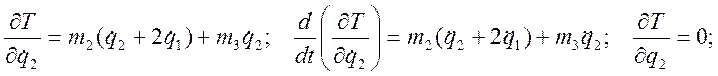
![]() ;
;
Пример 3.
|
|
Выражение для кинетической энергии системы имеет вид:
Получаем систему трех уравнений Лагранжа:
|
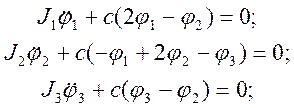 ;
;
Пример 4.
|
|
Выражение для кинетической энергии имеет вид:
Вычислив производные от кинетической энергии
|
получаем уравнение Лагранжа для этой системы:
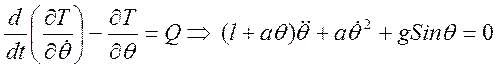 ;
;
Видно,
что отсюда при ![]() <<1 получаем классическое
уравнение колебаний математического маятника:
<<1 получаем классическое
уравнение колебаний математического маятника:
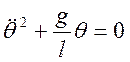
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.