Движение в центральном поле. Задача Кеплера

Лекция 6

Движение в центральном поле. Задача Кеплера.

Центральным называется поле, в котором действующие силы направлены по направлению к силовому центру. Таким свойством обладают кулоновские электростатические силы и гравитационные силы.

Закон всемирного тяготения (1) был окончательно подтвержден в экспериментах Г. Кавендиша (1798 г.). Была экспериментально измерена гравитационная константа, которая по современным данным:

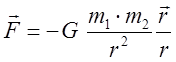                                          (1)

Здесь - массы тяготеющих тел,  - вектор, соединяющий первое тело со вторым. Знак минус означает, что сила направлена противоположно , это сила притяжения.

В данном гравитационном поле потенциальная энергия, как было показано в Л.5 (18)

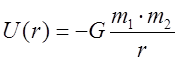                                         (2)

Момент импульса частицы.

Для понимания дальнейшего потребуется ввести новую физическую величину – момент импульса частицы. Будем называть моментом импульса векторное произведение радиус вектора на импульс частицы:

                                            (3)

В отличие от скалярного произведения результатом векторного произведения векторов является вектор.

Приведем некоторые свойства векторного произведения. Пусть - произвольные вектора и . Утверждается, что:

1) , вектор перпендикулярен плоскости, в которой лежат вектора .

2) Модуль . Или, длина вектора  равна площади параллелограмма, натянутого на вектора .  Из свойства 2), в частности, следует, что . И, вообще, векторное произведение параллельных векторов дает нулевой вектор.

Приведем также одно полезное правило вычисления двойного векторного произведения.

Иногда это правило называется правилом «бац» минус «цаб».

Определим момент импульса частицы, вращающейся в некоторой плоскости.

. Применив правило вычисления двойного векторного произведения, получим: . Последнее слагаемое равно нулю, т.к. вектор угловой скорости и радиус – вектор частицы перпендикулярны друг другу . Окончательно:

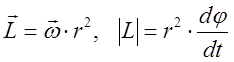.                                           (4)

Момент импульса частицы направлен вдоль направления угловой скорости .

Найдем скорость изменения момента импульса частицы:

.

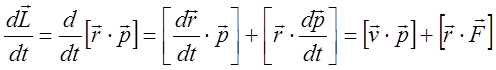Учитывая, что векторное произведение параллельных векторов равно 0: , получаем, что:

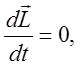     т.е.  .                               (5)

Момент импульса частицы в поле центральных сил сохраняется. Это фундаментальный закон сохранения наряду с законом сохранения импульса и законом сохранения энергии, как уже было доказано, выполняется в поле центральных сил. Из определения момента импульса следует: 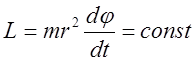. Покажем, что 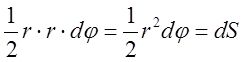, где - приращение площади, заметаемой радиус – вектором частицы. Определим секториальную скорость (см. рис. n3) как: 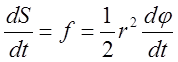 . Сравнивая (4) с выражением секториальной скорости находим, что:

                                          (6)

причем равенство выполняется не только по модулю, но и в направлении векторов, если определить направление плоскости, в которой происходит движение частицы. Постоянство момента импульса означает сохранение секториальной скорости. Приведем формулировку II-го закона Кеплера: площади, заметаемые радиус – вектором планеты, проведенным из Солнца за равные промежутки времени – одинаковы. (cм. рис. n4).

            Напомним, что потенциальная энергия  в поле тяготения 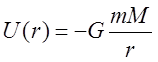, всюду далее, без ущерба для общности будем считать 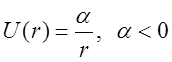. Действительно, как было показано в Л.5 в случае  -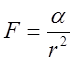

,

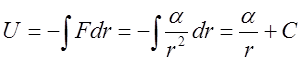При калибровке следует положить , следовательно .

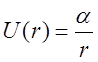Центральное поле является консервативным, поэтому полная энергия частицы, с массой равной приведенной массе (см. задача двух тел) сохраняется.

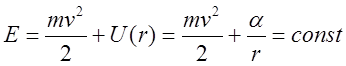                         (7)

Обозначим компоненты скорости  , тогда , поскольку . Закон сохранения энергии будет записываться в виде:

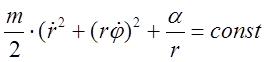, подставляя  окончательно имеем:

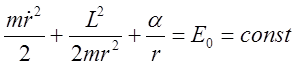                                  (8)

Обозначим 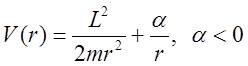, - эффективный потенциал. График  приведен на рис. n5. При малых радиусах вклад слагаемого пропорционального  становится гораздо большим нежели , поэтому при , . Напротив, при стремится к 0 из области отрицательных значений. Минимум достигает при .

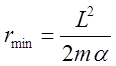Определим границы движения. Будем называть точками остановки значения координаты , при которых скорость становится равной нулю -  - радиальное движение останавливается.  В уравнении (8)   немедленно приводит к равенству  из которого возможно определить искомые координаты.

Рассмотрим характер движения частицы при различных значениях полной энергии .

1.  Пусть . Нетрудно видеть, что радиальное движение будет происходить в интервале радиусов . Такое движение называется инфинитным (неограниченным)

2.  Аналогично - существует единственная точка остановки. Движение инфинитно.

3.  Если , то существует две точки остановки. Движение ограничено, совершается в интервале . Говорят, что движение финитно (ограничено).

4.  Наконец, если положить , то две точки остановки стягиваются в одну.

Классификация траекторий.