§3.13 Движение точки под действием центральной силы. Законы Кеплера.
Секторная скорость, теорема площадей
Секторной
скоростью точки ![]() или
или ![]() относительно
центра О называют векторную величину, определяемую по формуле
относительно
центра О называют векторную величину, определяемую по формуле 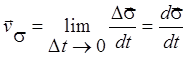
|
|
|
Тогда
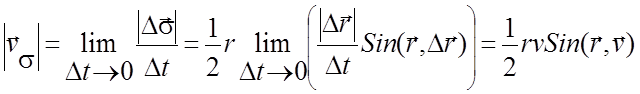 ,
,
то есть 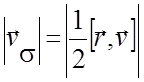
Направление
вектора ![]() также соответствует правилу векторного
произведения, так что
также соответствует правилу векторного
произведения, так что
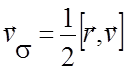
Согласно этому теорему об изменении кинетического момента точки можно записать в виде:
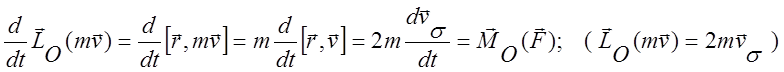
|
|
Центральной называют силу, действующую на точку, линия действия которой при движении точки все время проходит через некоторую неподвижную точку – центр силы. Центр силы может быть как притягивающим, так и отталкивающим. Для центральной силы ее момент относительно ее центра всегда равен нулю и
|
В проекциях на декартовы оси координат имеем:
![]()
здесь С1,С2,С3 – константы.
Умножая первое соотношение на x, второе – на y, третье – на z и складывая, получим:
С1x+С2y+С3z=0;
то есть координаты движущейся точки x,y,z удовлетворяют уравнению плоскости, проходящей через начало координат О.
Траектория точки, движущейся под действием центральной силы, является плоской кривой, лежащей в неподвижной плоскости, проходящей через центр силы.
Так
как ![]() , то
, то 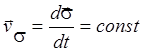 и
и
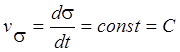 или
или ![]() .
.
Эта формула выражает интеграл площадей: при движении точки под действием центральной силы секторная скорость является постоянной величиной и, следовательно, заметаемая радиус-вектором площадь пропорциональна времени.
Сравним это со вторым законом Кеплера: «Секторная скорость каждой планеты относительно Солнца постоянна».
Поместим начало координат в центр силы и запишем законы сохранения кинетического момента и механической энергии:
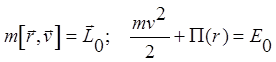
Введем на плоскости, в которой происходит движение, полярные координаты и перепишем эти законы сохранения в виде:
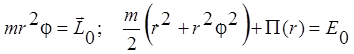
Эти выражения часто называются
интегралом площадей и интегралом энергии. Исключая ![]() из
интеграла энергии с помощью интеграла площадей получим:
из
интеграла энергии с помощью интеграла площадей получим:
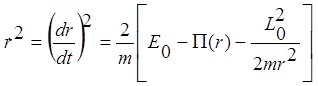
Разделив в этом уравнении переменные после интегрирования будем иметь:
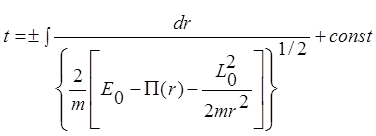 (3.13.1)
(3.13.1)
Из этого выражения в принципе можно определить зависимость r = F(t).
Из
интеграла площадей также можно получить, что 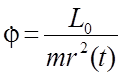 (
(![]() имеет постоянный знак, зависящий от знака L0, что означает, что полярный угол
меняется монотонно) и после разделения переменных и интегрирования иметь:
имеет постоянный знак, зависящий от знака L0, что означает, что полярный угол
меняется монотонно) и после разделения переменных и интегрирования иметь:
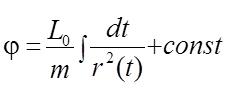
Интеграл момента позволяет найти уравнение траектории, если с его помощью в интеграле энергии исключить dt, а затем вычислить квадратуру:
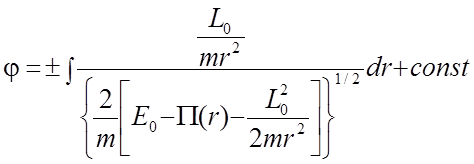 (3.13.2)
(3.13.2)
Выбор
знаков в (3.13.1) и (3.13.2) диктуется начальными условиями, в частности, знак
в (3.13.1) определяется знаком ![]() в начальный момент времени.
в начальный момент времени.
Таким образом, мы получили общее решение задачи движения точки в поле центральной силы. Оно справедливо для любой центральной силы, зависящей только от расстояния до центра силы.
Для вывода первого и третьего законов Кеплера потенциальную энергию возьмем в виде:
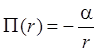 (здесь
(здесь ![]() для
гравитационного поля и
для
гравитационного поля и ![]() для электростатического поля).
для электростатического поля).
Подставляя в уравнение траектории (3.13.2) указанную зависимость потенциальной энергии от расстояния до центра силы и проводя несложные преобразования, перепишем это уравнение в виде:
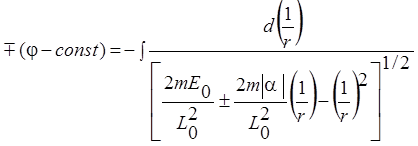
здесь знак “+” под интегралом соотвествует случаю a > 0 (сила притяжения) и знак “-” соответствует случаю a < 0 (сила отталкивания).
Вводя
вместо постоянных E0 и L0 положительные по определению
постоянные 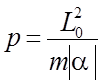 и
и 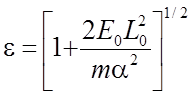 перепишем
это уравнение в виде:
перепишем
это уравнение в виде:
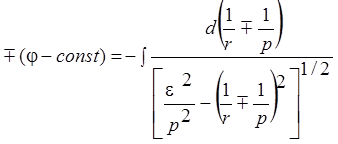
и в результате интегрирования получим:
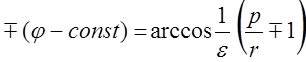
Опуская знак “-” перед j в виду четности косинуса получим окончательно уравнение орбиты:
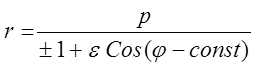 (3.13.3) ;
(3.13.3) ;
где по прежнему знак “+” имеем для a > 0 и знак “-” для a < 0. Величина p называется параметром орбиты, а e - эксцентриситетом орбиты. Если полярную ось направить к ближайшей к центру силы точку траектории, const=0.
Из аналитической геометрии известно, что уравнение (3.13.3) при e>1 является уравнением гиперболы (это соответствует случаю E0 > 0 – точка приближается к центру силы из бесконечности, где имеет положительную начальную скорость), при e=1 является уравнением параболы (случай E0 = 0 – точка приближается к центру силы из бесконечности, где имеет нулевую начальную скорость) а при e<1 – эллипсом. Последний случай соотвествует ситуации, когда E0 < 0 (точка не можен уйти на бесконечность и движется в некоторой окрестности центра силы). Это как раз и является первым законом Кеплера: «Планеты движутся по эллиптическим траекториям в одном из фокусов которых находится Солнце». Следует отметить, что на самом деле планеты движутся по эллиптическим траекториям в одном из фокусов которого находится центр масс солнечной системы.
При движении по эллипсу минимальное и максимальное расстояние до центра силы равны:
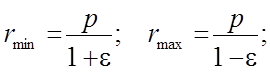
а для полуосей эллипса из аналитической геометрии имеем:
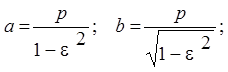 то
есть
то
есть 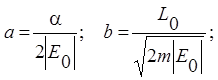
то есть большая полуось орбиты зависит от полной энергии E0 и не зависит от начального значения кинетического момента точки L0.
Запишем еще раз кинетический момент точки через секторную скорость:
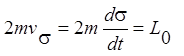
Разделяя переменные, интегрируя это выражение по полному периоду обращения и учитывая, что площадь эллипса равна pab, найдем
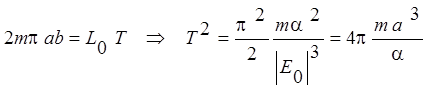 ;
;
А это и есть третий закон Кеплера (пропорциональность квадратов периодов обращения планет вокруг Солнца кубам больших полуосей орбит).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.