Канонические уравнения Гамильтона, фазовое пространство

§3.19 Канонические уравнения Гамильтона, фазовое пространство

            Обобщенным импульсом называется величина 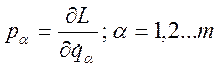. Здесь L-функция Лагранжа механической системы (иногда ее называют избытком кинетической энергии над потенциальной), m-число степеней свободы механической системы.

            Определим новую функцию, которая называется функцией Гамильтона:

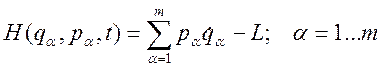;       (3.19.1)

            Запишем дифференциал от правой части (3.19.1) :

;

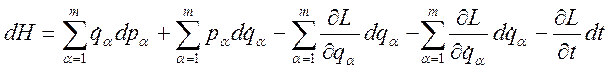            Последние три слагаемых здесь есть дифференциал от функции Лагранжа как функции обобщенных координат, скоростей и времени: . Второе и четвертое слагаемое по определению импульса одно и то же. Таким образом, дифференциал от (3.19.1) у нас имеет вид:

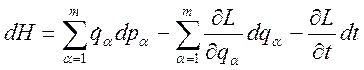;          (3.19.2)

            С другой стороны, H есть функция переменных q_a, p_a, t. Поэтому дифференциал от левой части (19.1) будет иметь вид:

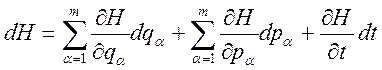;       (3.19.3)

            Отсюда, приравнивая коэффициенты при одинаковых дифференциалах в (3.19.2) и (3.19.3), имеем:

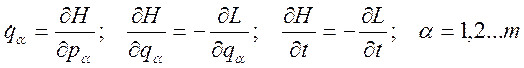_;            (3.19.4)

            Из уравнений Лагранжа следует: 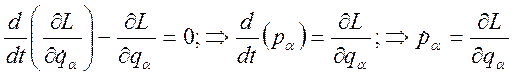 или, учитывая  третий элемент в (3.19.4), .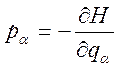

            Окончательно запишем систему уравнений Гамильтона (систему канонических уравнений):

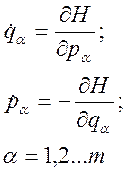
            Эти уравнения эквивалентны уравнениям Лагранжа, только их 2m штук. Однако уравнения Гамильтона имеют более симметричную форму и являются системой дифференциальных уравнений первого порядка. Уравнения Гамильтона служат для определения q_a(t) и p_a(t), если для них дополнительно заданы начальные условия, по которым можно определить постоянные интегрирования.

            Формализм уравнений Гамильтона широко применяется в квантовой и статистической механике.

Пример.

Составить уравнения Гамильтона для системы с одной степенью свободы, для которой  кинетическая и потенциальная энергия выражаются в форме:

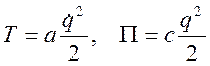,            где a и c постоянные положительные величины.

Решение.

            Вычисляем функцию Лагранжа. Имеем

.

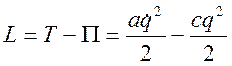            Определим обобщенный импульс p. Получаем

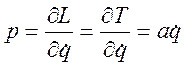;    (3.19.5)

            так как P не зависит от обобщенной скорости.

            Для функции Гамильтона, согласно ее определению (3.19.1), имеем

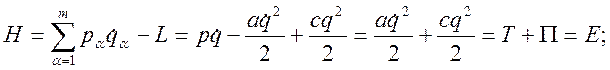
то есть в рассматриваемом случае функция Гамильтона H равна полной механической энергии E.

            Для составления уравнений Гамильтона выразим функцию H через переменные q и p, используя (3.19.5). Получим

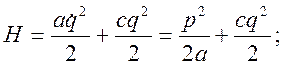            (3.19.6)

            Из (19.6) путем дифференцирования имеем:

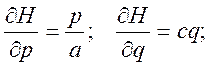
            Подставляя эти значения производных в уравнения Гамильтона, получим следующую систему уравнений:

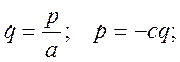       (3.19.7)

            Из системы уравнений Гамильтона (3.19.7) путем дифференцирования первого уравнения по времени и подстановки  в полученное выражение из второго уравнения получим дифференциальное уравнение для определения q:

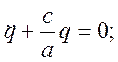
              Это уравнение является классическим уравнением гармонических колебаний (например, груз массы m[в этом случае роль величины a играем масса груза], закрепленный на пружине жесткости c), где коэффициент при q есть квадрат круговой частоты колебаний.

            Фазовым пространством называется воображаемое пространство 2m (m-число степеней свободы механической системы) измерений, по координатным осям которого откладываются обобщенные координаты q_a и импульсы p_a механической системы.

            В данный момент времени состояние механической системы изображается в фазовом пространстве одной фазовой точкой. С течением времени эта точка перемещается по так называемой фазовой траектории (состояние системы изменяется).

            Через каждую точку фазового пространства проходит только одна фазовая траектория данной механической системы. Это следует из единственности решений уравнений Гамильтона (Лагранжа, Ньютона). Этим свойством не обладает пространство, точки которого задаются совокупностью значений обобщенных координат q_a (так называемое конфигурационное пространство).

§3.20 Принцип наименьшего действия

            Имеем механическую систему с m степенями свободы, диссипативные силы отсутствуют. Ее движение описывается системой уравнений Лагранжа 2-го рода:

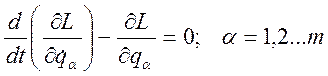;    (3.20.1)

            Умножим уравнения (20.1) на соответствующие   и, складывая, получим

;

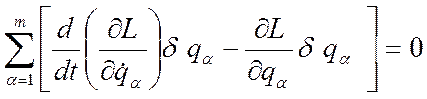            Учитывая независимость операций дифференцирования по времени  и варьирования по координатам при фиксированном времени имеем:

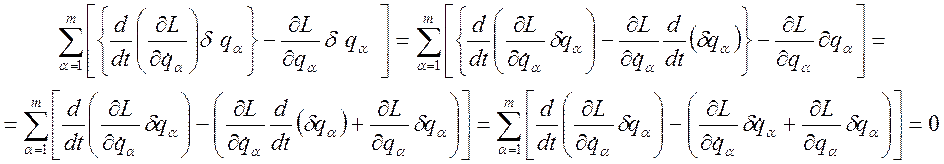
            Таким образом, получаем:

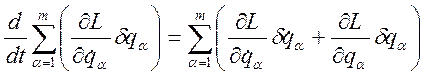;            (3.20.2)