Механика \ Механика

Канонические уравнения Гамильтона, фазовое пространство, страница 2

            С другой стороны, функция Лагранжа является функцией обобщенных координат , скоростей и времени t, тогда вариация функции Лагранжа имеет вид:

 

;

 

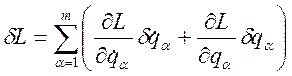                  Тогда (3.20.2) можно переписать в виде:

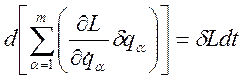;      (3.20.3)

            После интегрирования от момента времени t=t0 до момента времени t=t1 из (3.20.3) получим:

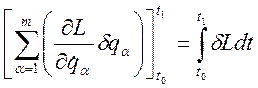;    (3.20.4)

   Пусть в фазовом пространстве в момент времени t0 состояние механической системы изображается точкой A, а в момент времени t1 – точкой B. Пусть действительной траекторией движения системы в фазовом пространстве будет кривая A-0-B. Можно вообразить себе возможные перемещения по траекториям A-1-B, A-2-B,… A-n-B по которым система за тот же интервал времени перейдет из состояния A в состояние B. Потребуем, чтобы все траектории пересекались в точках A и B. Действительные и возможные перемещения совпадут в моменты времени t = t0, t1, если будет иметь место

   (3.20.5)

            С учетом этого левая часть (3.20.4) обратится в ноль и само выражение (3.20.4) перепишется в виде:

,

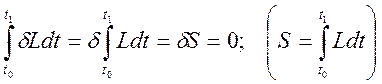где S называется функций действия.

            В итоге получаем: функция действия на действительной траектории имеет экстремальное значение по сравнению с ее значениями на кинематически возможных перемещениях, совершаемых за тот же промежуток времени между теми же состояниями механической системы. Можно показать, что это минимум энергетического функционала S, которым является функция действия (). В результате мы сформулировали так называемый принцип наименьшего действия.

            Можно и из принципа наименьшего действия получить уравнения движения в форме уравнений Лагранжа:

.

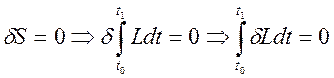            Развертывая вариацию  получим:

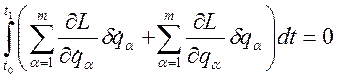;   (3.20.6)

            Применим к слагаемым первой суммы в (3.20.6) интегрирование по частям и свойство независимости операций  и :

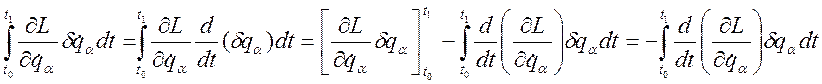;           (3.20.7)

            Член с подстановкой в (3.20.7) в моменты времени t=t0 и t=t1 обращается в ноль, как и прежде, в силу (3.20.5).

            Имея в виду (3.20.7) после подстановки его в (3.20.6) найдем:

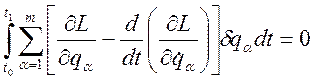;      (3.20.8)

            Так как все  между собой независимы, а интервал интегрирования выбирается произвольно, то (3.20.8) может иметь место только в случае

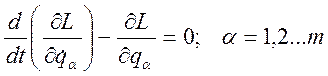
            Можно также из принципа наименьшего действия получить канонические уравнения Гамильтона:

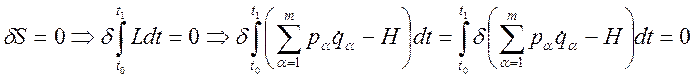;            (3.20.9)

            Развертывая вариацию в (3.20.9) получим:

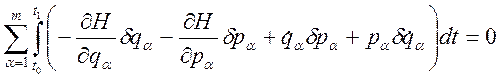;            (3.20.10)

            Последнее слагаемое в (3.20.10) при интегрировании по частям  запишем в виде:

;

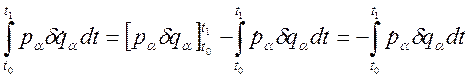            то есть (3.20.10) перепишется в виде:

;

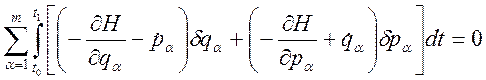            А это может быть, как и раньше, только в случае

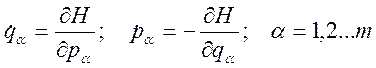
§3.21 Классификация принципов динамики

            Под принципом понимается такое аксиоматическое положение, которое обладает достаточной общностью, является основным положением, из которого как логические следствия вытекают все остальные положения механики (законы Ньютона можно назвать в этом случае принципами).

            Все принципы динамики можно разделить на четыре категории делением на «вариационный/невариационный» и «интегральный/дифференциальный»:

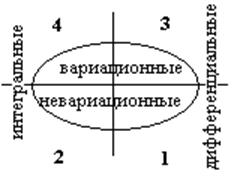
            Невариационный принцип есть утверждение о некотором для всех движений свойстве, которое имеет место или для данного момента времени в случае дифференциального или для конечного интервала времени в случае интегрального принципа.

            Вариационные принципы дают способ отличить действительное перемещение системы от других (возможных) перемещений. Для любого вариационного принципа должна иметься некоторая функция, обладающая для действительного перемещения экстремальными свойствами по сравнению с возможными перемещениями. Получение уравнений движения из вариационного принципа, следовательно, сводится к вариационной задаче при некоторых дополнительных условиях.

            Дифференциальные и интегральные вариационные принципы также дают критерий для определения действительного перемещения, отнесенный к данному моменту времени или к конечному интервалу времени.

            Примерами различных категорий принципов могут служить:

  1. Принципы (законы) Ньютона (дифференциальный невариационный принцип),
  2. Принцип (закон) сохранения механической энергии (интегральный невариационный принцип),
  3. Принцип Даламбера (дифференциальный вариационный принцип),
  4. Принцип наименьшего действия  (интегральный вариационный принцип).
Скачать файл