§ 2.5. Движение: абсолютное, относительное, переносное. Теорема Эйлера. Угловая скорость.
Дополнительно к неподвижным осям Oxyz (система S) введем в рассмотрение некоторое подвижное твердое тело и неизменно связанную с ним систему прямоугольных осей координат O’x’y’z’ (система S’).
Движение точки относительно подвижной системы осей S’ называется относительным движением.
Движение точки относительно неподвижных осей S называется абсолютным движением.
Переносным движением точки за интервал времени (t,t+Dt) называется то движение по отношению к осям S, которая эта точка имела бы, если бы в момент времени t и на интервал (t,t+Dt) она была неизменно связана с подвижной системой осей и, следовательно, перемещалась бы вместе с этой системой.
Траектория, скорость и ускорение называются абсолютными, относительными или переносными, смотря по тому, относятся ли они к движению абсолютному, относительному или переносному.
Теорема Эйлера: Если относительно системы S система S' имеет одну неподвижную точку, то перемещение S' из одного произвольного положения в любое другое может быть совершено одним поворотом на определенный угол относительно оси, проходящей через эту неподвижную точку.
Для
доказательства достаточно показать возможность перевода одним поворотом дуги,
например, ![]() .
.
|
|
è |
|
|
|
|
Проведем два экватора: a, перпендикулярный середине x1'x2', и b, перпендикулярный середине z1'z2'. Получим две точки пересечения этих экваторов – с и d. Dx1'z1'd = Dz2'x2'd (так как x1'z1' = x2'z2', а x1'd = x2'd в силу того, что точка d лежит на экваторе, перпендикулярном середине x1'x2', z1'd = z2'd по той же причине) Таким образом, Ðx1'dz1' = Ðz2'dx2' и угол между дугами x1'd и x2'd равен углу между дугами z1'd и z2'd, то есть нужно повернуть x1'z1' относительно оси dO'c на угол x1'dz1' (или равный ему z2'dx2') |
||
|
|
|||
Теорема Эйлера справедлива и для конечных поворотов и для бесконечно малых. Хотя последовательность бесконечно малых поворотов может быть любой – результат будет тем же, конечные же повороты не коммутируют. Это тем более справедливо для бесконечно малых поворотов, чем ближе дуги, описываемые какой-либо точкой, к хордам, соединяющим концы дуг.
При рассмотрении задач о движении тела с одной закрепленной точкой, которые имеют большое практическое значение, для определения (фиксации) положения системы S' относительно S широко используются три угла Эйлера.
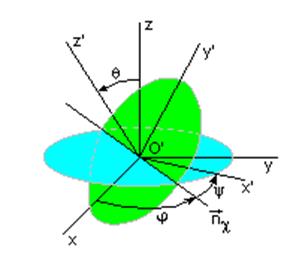
Пересечение плоскостей O'xy и O'x'y' дает прямую,
которую называют линией узлов (орт линии узлов - ![]() ).
Первый угол Эйлера j - угол между осью O'x и линией узлов. Второй угол y - угол между линией узлов и осью O'x'. Третий угол q - угол между осями O'z и O'z'.
).
Первый угол Эйлера j - угол между осью O'x и линией узлов. Второй угол y - угол между линией узлов и осью O'x'. Третий угол q - угол между осями O'z и O'z'.
Эти три угла однозначно определяют положение системы S' относительно S
Таким образом, при бесконечно малом повороте системы S' относительно S на углы dj,dy,dq (некоторые из них могут быть равными нулю) их можно заменить одним поворотом на угол dc вокруг некоторой оси, проходящей через точку O'.
Введем в рассмотрение вектор бесконечно малого поворота:
![]() (здесь
(здесь ![]() направлен по оси вращения по правилу
правого винта)
направлен по оси вращения по правилу
правого винта)
Величина
и направление вектора dc при сложном движении могут изменяться. Ось ![]() называется осью мгновенного вращения.
Посмотрим, что происходит с ортами системы S' при ее повороте на угол
называется осью мгновенного вращения.
Посмотрим, что происходит с ортами системы S' при ее повороте на угол ![]()
|
|
Угловую
скорость вращения
Тогда |
§ 2.6. Сложное движение точки.
|
|
Рассмотрим движение точки по траектории в
пространстве (точка находится в положении М). Будем рассматривать параметры
ее движения из неподвижной системы Oxyz и подвижной системы O'x'y'z' (начало
отсчета О' может двигаться поступательно и система O'x'y'z' может совершать
вращение относительно оси, проходящей через точку О' с угловой скоростью |
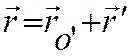
продифференцировав это соотношение по времени, получим:
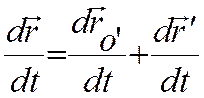
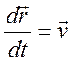 -
абсолютная скорость точки (относительно системы S),
-
абсолютная скорость точки (относительно системы S),
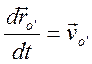 -
скорость начала координат S' относительно S,
-
скорость начала координат S' относительно S,
![]() не
является скоростью точки М относительно системы S', так как орты этой системы
являются функциями времени.
не
является скоростью точки М относительно системы S', так как орты этой системы
являются функциями времени.
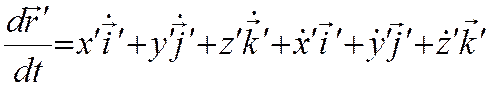 ,
,
используя формулы (2.5.1) будем иметь:
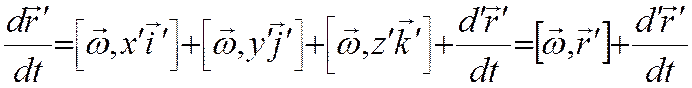
Последнее слагаемое означает, что производная берется
при неизменных ортах системы O’x’y’z’, 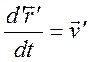 .
.
Теперь для скоростей имеем:
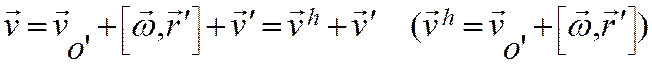
здесь vh-переносная, v – абсолютная, v’ – относительная скорость точки, то есть получена связь этих скоростей. Переносная скорость состоит из двух слагаемых: первое присутствует в том случае, если подвижная система отсчета движется поступательно, второе появляется в том случае, если подвижная система отсчета совершает вращение.
Для получения связи ускорений продифференцируем по времени соотношение для скоростей:
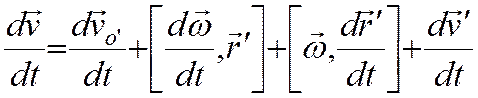
![]() - абсолютное ускорение,
- абсолютное ускорение, ![]() - ускорение начала координат S’
относительно S.
- ускорение начала координат S’
относительно S.
Используем соотношение 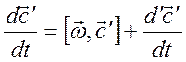 ,
ранее полученное для
,
ранее полученное для ![]() и справедливое для любого
вектора, разлагаемого по ортам S’, которая вращается относительно неподвижной
системы отсчета.
и справедливое для любого
вектора, разлагаемого по ортам S’, которая вращается относительно неподвижной
системы отсчета.
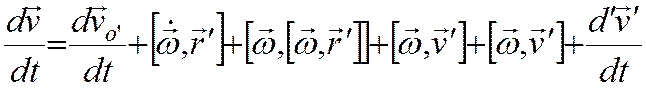
или
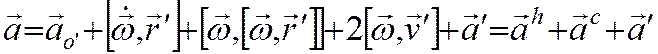
здесь переносное ускорение состоит из трех компонент (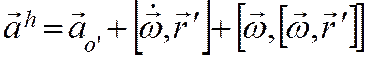 ), первая имеет место, если подвижная
система отсчета движется поступательно и при этом неравномерно, вторая
появляется при неравномерном вращении подвижной системы отсчета и третья,
называемая центростремительным ускорением, присутствует всегда, если подвижная
система отсчета просто вращается.
), первая имеет место, если подвижная
система отсчета движется поступательно и при этом неравномерно, вторая
появляется при неравномерном вращении подвижной системы отсчета и третья,
называемая центростремительным ускорением, присутствует всегда, если подвижная
система отсчета просто вращается.
Кориолисово ускорение (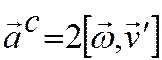 )
присутствует у точки при двух условиях: если подвижная система отсчета
вращается и точка движется относительно подвижной системы отсчета и вектор
)
присутствует у точки при двух условиях: если подвижная система отсчета
вращается и точка движется относительно подвижной системы отсчета и вектор ![]() не параллелен вектору
не параллелен вектору ![]() .
.
Кориолисово ускорение на Земле действует на тело,
движущееся по поверхности всегда за исключением экваториальной области при
движении С « Ю (![]() параллельно
параллельно ![]() ) или если v’=0 или w=0, первое имеем для всех неподвижных тел. Даже на неподвижное тело
действует ускорение
) или если v’=0 или w=0, первое имеем для всех неподвижных тел. Даже на неподвижное тело
действует ускорение ![]() , равное по модулю w2r, где r - расстояние от точки до оси вращения, т.е. вес тела зависит от широты
(w2r=(7 x 10-5)2
x 6.3 x 106=0.03 м/с2»0.3% от g).
, равное по модулю w2r, где r - расстояние от точки до оси вращения, т.е. вес тела зависит от широты
(w2r=(7 x 10-5)2
x 6.3 x 106=0.03 м/с2»0.3% от g).
a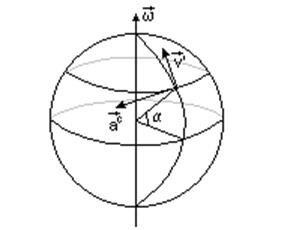 = 45o
= 45o
v’ = 1 м/с
w = 0.00007 рад/с
m = 75 кг
Fc = -mac=-2mwv’Sina=10-4 H
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.