The Harmonic Oscillator

THE HARMONIC OSCILLATOR      

·         Nearly any system near equilibrium can be approximated as a H.O.

·         One of a handful of problems that can be solved exactly in quantum mechanics

examples

 

Classical H.O.

 

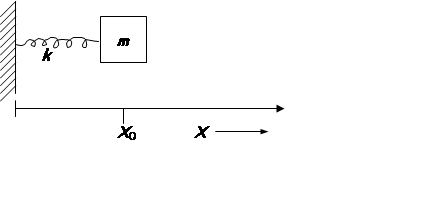Hooke’s Law:

(restoring force)

                   

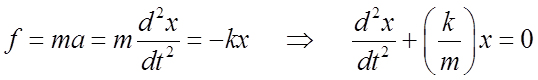
Solve diff. eq.:       General solutions are sin and cos functions

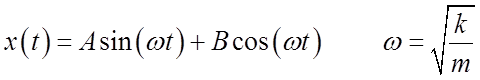
          or can also write as

                    

          where  A and B  or   C and f   are determined by the initial conditions.

          e.g.          

spring is stretched to position x₀ and released at time t = 0.

Then

                              

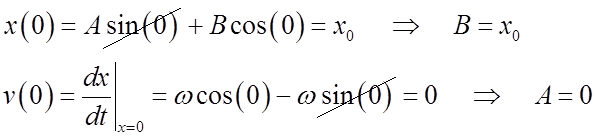
So          

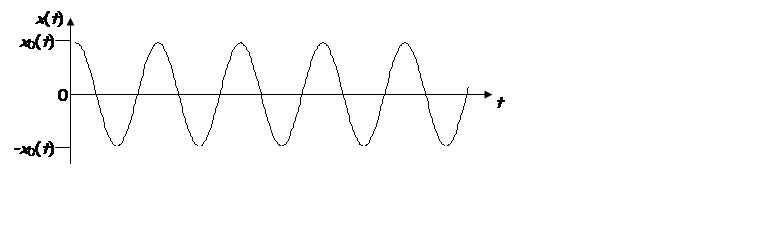
Spring oscillates with frequency    

and maximum displacement   from equilibrium

Energy of H.O.

Kinetic energy º K

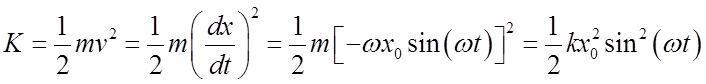
Potential energy º U

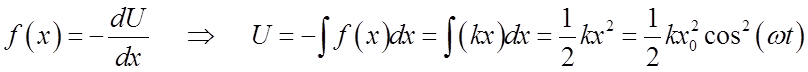
Total energy = K + U = E

 

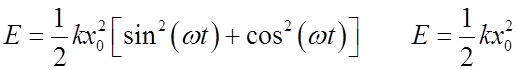
Most real systems near equilibrium can be approximated as H.O.

 

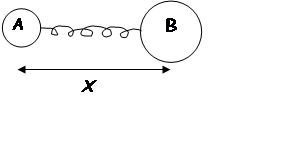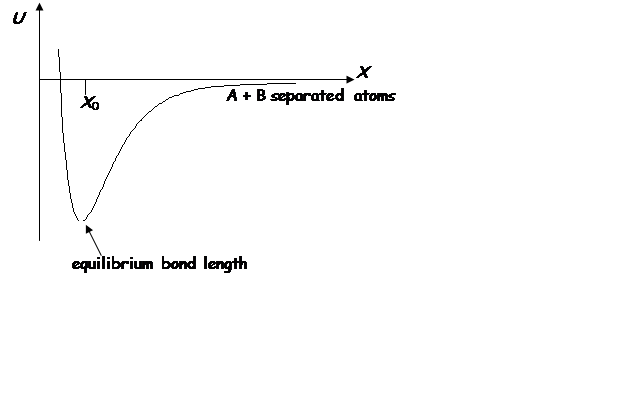
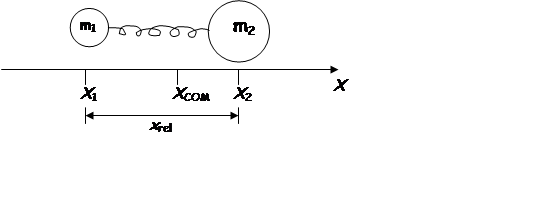
e.g.          Diatomic molecular bond

 

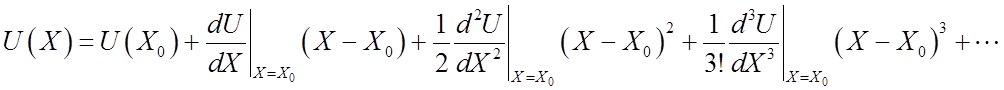
Redefine      and   

 

At eq.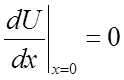     

For small deviations from eq.         

\ 

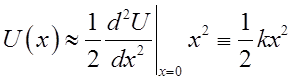
Total energy of molecule in 1D

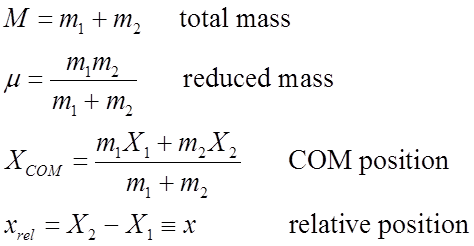
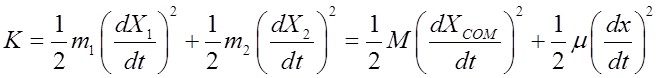
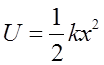
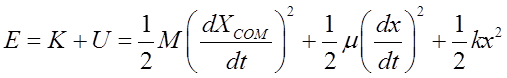
COM coordinate describes translational motion of the molecule

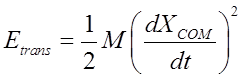
QM description would be free particle or PIB with mass M

We’ll concentrate on relative motion (describes vibration)

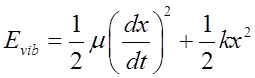
and solve this problem quantum mechanically.

THE QUANTUM MECHANICAL HARMONIC OSCILLATOR    

 

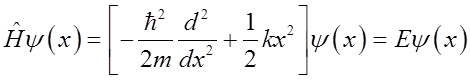
                                     K            U

 

          Note: replace m with m (reduced mass) if

          Goal: Find eigenvalues E_n and eigenfunctions y_n(x)

          Rewrite as:

                              

 

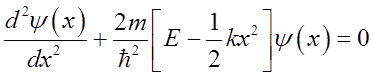
                                         This is not a constant, as it was for P-I-B,

                                         so sin and cos functions won’t work.

TRY:                     (gaussian function)

         

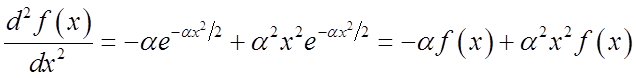
or rewriting,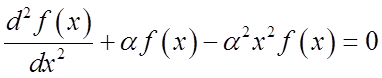         

which matches our original diff. eq. if

                     \      

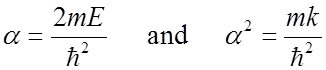
We have found one eigenvalue and eigenfunction

          Recall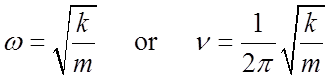          

                     \      

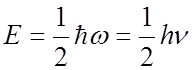
          This turns out to be the lowest energy: the “ground” state

          For the wavefunction, we need to normalize:

                     where N is the normalization constant

         

 

                                                     

          \            

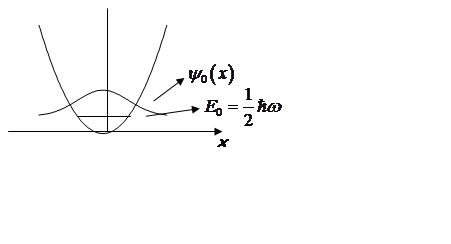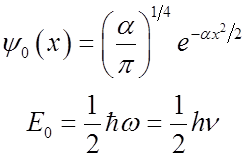
Note  is symmetric. It is an even function:

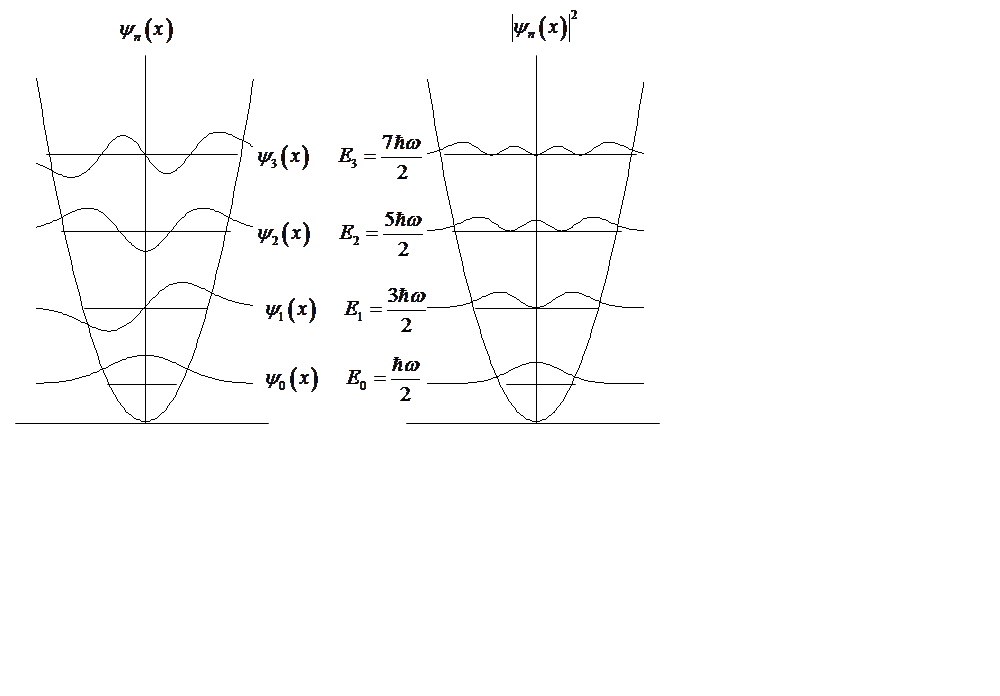
There are no nodes, & the most likely value for the oscillator displacement is 0.

So far we have just one eigenvalue and eigenstate. What about the others?

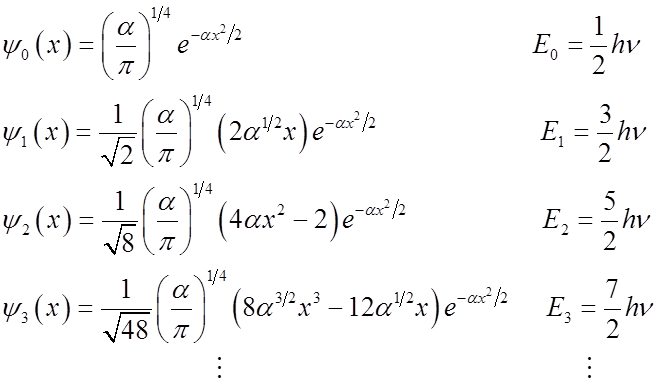
                                                   with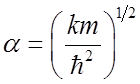  

These have the general form

 

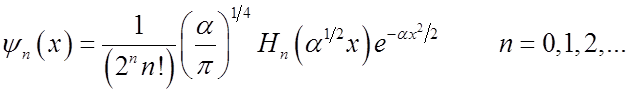
                     Normalization                   Gaussian

Hermite polynomial

 

Energies  are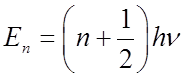         

                               Note E increases linearly with n.

          Þ       Energy levels are evenly spaced

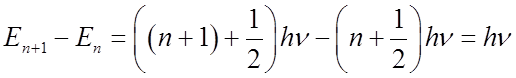                        regardless of n

          There is a “zero-point” energy            

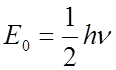
          E = 0 is not allowed by the Heisenberg Uncertainty Principle.

Symmetry properties of y’s

                 are even functions          

                  are even functions          

          Useful properties:           (even) ×(even) = even

                                                   (odd) ×(odd) = even

                                                   (odd) ×(even) = odd