


















Задачи, рекомендуемые для подготовки к гос. экзамену
!!!!!
Данный файл был составлен несколькими студентами группы ПМ-12 по материалу списков типовых задач к экзаменам по мат. анализу 1-3 семестров, составленных С. Е. Рояк. Он был составлен по рекомендациям преподавателя, но не прошел окончательной проверки, поэтому за все ошибки и опечатки Светлана Ефимовна ответственности не несет!
1. Предел функции
1. Используя замечательные пределы, докажите, что
1) 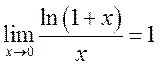 , 2)
, 2) 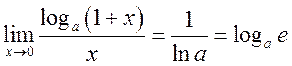 , 3)
, 3) 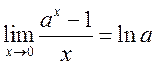 , 4)
, 4)
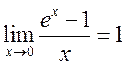 ,
,
5) 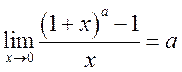 , 6)
, 6) 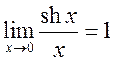 , 7)
, 7) 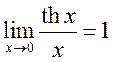 , 8)
, 8)
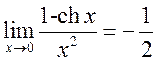 .
.
2. Используя неравенство ![]()
![]() , докажите, что
, докажите, что 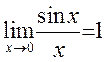 .
.
3. Докажите, что ![]() не существует.
не существует.
4. Найти:
1) 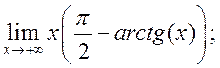 2)
2) ![]()
3) 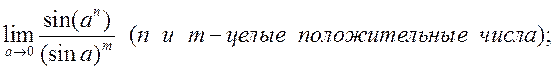
4) 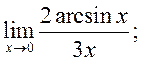 5)
5)
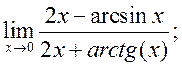 6)
6) 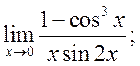 7)
7) 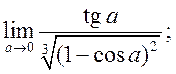
8) 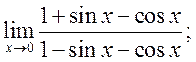 9)
9)
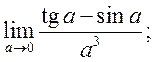 10)
10) 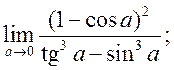
11) 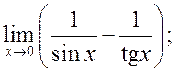 12)
12)
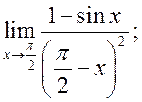 13)
13) 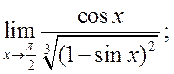
14) 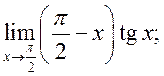 15)
15)
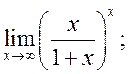 16)
16) 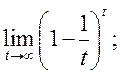 17)
17) 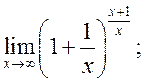
18) 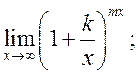 19)
19)
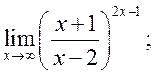 20)
20)
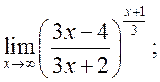 21)
21) 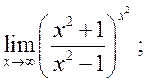
22) 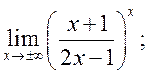 23)
23)
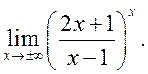
Задачи на вычисление пределов в больших количествах можно найти в индивидуальных заданиях (должна быть целая тетрадь!).
2. Непрерывность функций
1. Найти ![]() :
:
1)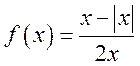 ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() ;
;
4) ![]() ,
,![]() ; 5)
; 5) ![]() ,
, ![]() ; 6)
; 6) 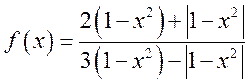 ,
, ![]() ;
;
7)![]() ,
,![]() ; 8)
; 8)![]() ,
, ![]() .
.
2. Функция f определена в
окрестности точки ![]() . Доопределить функцию f так, задав
. Доопределить функцию f так, задав ![]() , чтобы получившаяся
функция была непрерывна в точке
, чтобы получившаяся
функция была непрерывна в точке ![]() , если:
, если:
1)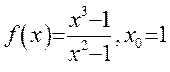 ; 2)
; 2)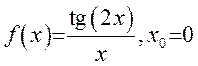 ; 3)
; 3)![]() ;
;
4)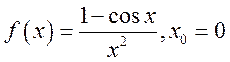 ; 5)
; 5) 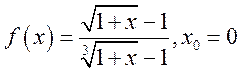 ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8)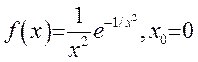 .
.
3. Доказать,
пользуясь неравенством ![]() , непрерывность функции
y, если: К10.6
, непрерывность функции
y, если: К10.6
а)![]() , б)
, б)![]() , в)
, в) ![]() .
.
4.
Доказать, что функция ![]() непрерывна в каждой точке
непрерывна в каждой точке ![]() и непрерывна слева в точке
и непрерывна слева в точке ![]() .
.
5(!!).
При каком значении a функция ![]() будет непрерывна, если:
будет непрерывна, если:
1) 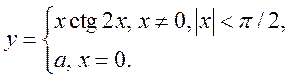 2)
2)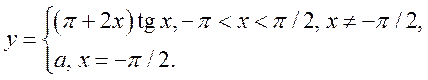
3) 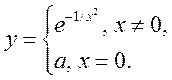 4)
4) 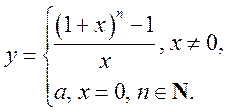 5)
5) 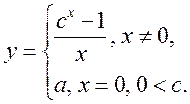
6) 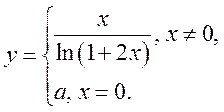 7)
7)
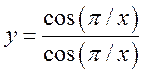 , 8)
, 8) 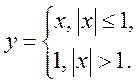
9)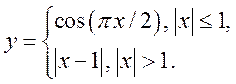
3. Задачи на наибольшее и наименьшее значения
1.
Пусть ![]() . В с.152N115
. В с.152N115
1) Найти множество на прямой Oy, являющееся образом множества:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , е)
, е) ![]() , ж)
, ж) ![]() ,
,
з) ![]() , и)
, и) ![]() .
.
2) Найти множество на прямой Ox, являющееся прообразом множества:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() .
.
2. Доказать ограниченность функций:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]()
3. Доказать неограниченность функций:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]()
4. Найти ![]() ,
, ![]() , а также
, а также ![]() ,
, ![]() , если последние существуют:
, если последние существуют:
1)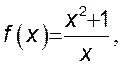 а)
а) ![]() , б)
, б) ![]() , в)
, в)![]() ;
;
2)
![]() ;
;
3) 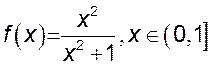 ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) 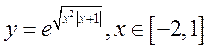 ; 7)
; 7)
![]() ; 8)
; 8)![]() ;
;
9)![]() ; 10)
; 10)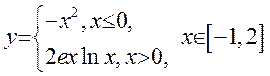 ;
;
11)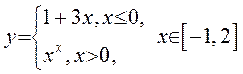 ; 12)
; 12)![]() ; 13)
; 13)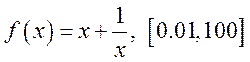 .
.
Замечание: сколько точек надо исследовать?? Только,
где ![]() или еще?...
или еще?...
5. Доказать, что существует ![]() , но не
существует
, но не
существует ![]() , и найти
, и найти ![]() , если:
, если:
1) 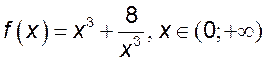 , 2)
, 2) 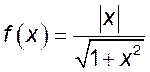 , 3)
, 3) 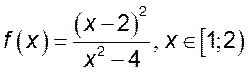
6. Доказать, что существует ![]() , но не
существует
, но не
существует ![]() , и найти
, и найти ![]() , если:
, если:
1) 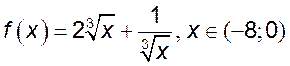 , 2)
, 2) 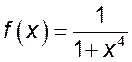 , 3)
, 3) 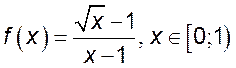
7. Найти экстремумы функций:
1) 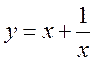 , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4)![]() , 5)
, 5)![]() , 6)
, 6) 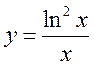 ,
,
7) 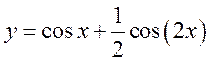 , 8)
, 8) 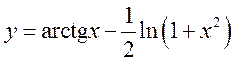 , 9)
, 9) ![]() , 10)
, 10) ![]() .
.
4. Бесконечно большие и бесконечно малые функции
1. Верно ли равенство:Бс.54
1) ![]() при
при ![]() , если:
, если:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]()
2) ![]() при
при ![]() , если:
, если:
а) ![]() , б)
, б) ![]() , в)
, в) ![]()
3) ![]() при
при ![]() , если:
, если:
а) ![]() ; б)
; б) ![]() , в)
, в) ![]() , г)
, г) ![]()
4) ![]() при
при ![]() , если:
, если:
а)![]() ; б)
; б)![]() , в)
, в) ![]()
3) ![]() при
при ![]() , если:
, если:
а) ![]() ; б)
; б) ![]() , в)
, в) ![]() , г)
, г) ![]() ,
,
д) ![]()
2. Определить порядок n бесконечно большой функции: К9.49
а) 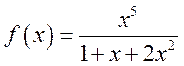 , при
, при ![]() ; б)
; б) ![]() , при
, при ![]() ;
;
в) 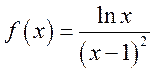 , при
, при ![]() ; г)
; г) ![]() , при
, при ![]() ;
;
д) 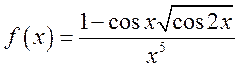 , при
, при ![]() .
.
3. Определить порядок n бесконечно малой функции: К9.48
а) ![]() , при
, при ![]() ; б)
; б) ![]() , при
, при ![]() ;
;
в) ![]() , при
, при ![]() ; г)
; г) ![]() , при
, при ![]() ;
;
д) ![]() при
при ![]() ; е)
; е) 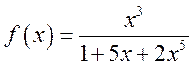 , при
, при ![]() .
.
А также:
Демидович №№ 646, 647, 648, 650, 651а)-г), 653-658 (выделение главной части вида…, доказательство одного из свойств символов Ландау…)
5. Формула Тейлора
Вычислить предел, используя формулу Тейлора:
<Б с.124 N 47,
63, 64>1) 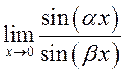 , 2)
, 2) 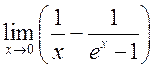 , 3)
, 3) 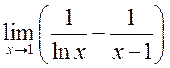 , 4)
, 4) 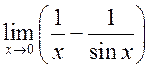 (!!!!≠0??),
(!!!!≠0??),
5) 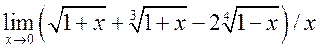 ,
6<K19.4 1> 6666)
,
6<K19.4 1> 6666)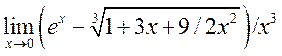 ,
,
7) 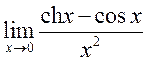 ,
8)
,
8) 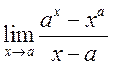 , 9)<К 9.57> 99
, 9)<К 9.57> 99![]() , 10)
, 10) 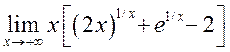 ,
,
11) ![]() ;
<К 9.17 56, 59> 12)
;
<К 9.17 56, 59> 12) 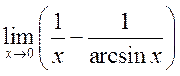 ,
13)
,
13) 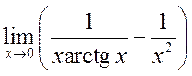 ,
,
<К 19.1 2, 5> 14)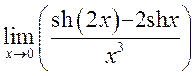 , 15)
, 15) 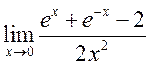 ; <Д 1398, 1405,
1406> 16)
; <Д 1398, 1405,
1406> 16) 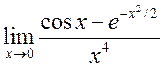 ,
,
!!: 17)<Б с.124 N67> 151
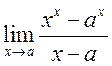 , 18<Б с.128 N73 б, в> 16)
, 18<Б с.128 N73 б, в> 16) 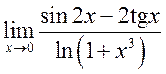 ,
,
19) 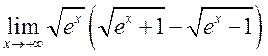 (кстати,
этот номер в образце билетов!),
(кстати,
этот номер в образце билетов!),
<К 9.58 1, 2,
3, 5> 20)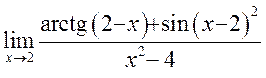 , 21)
, 21) 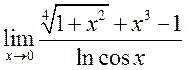 , 22)
, 22) 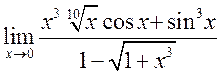 ,
,
23) 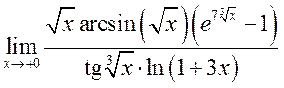 ,
24)
,
24)
<K17.58, 61>22 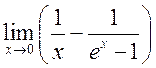 , 25)
, 25) 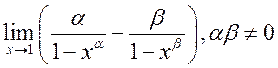 ,
,
<К 19.2 1, 2,
6>26) 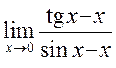 , 27)
, 27) 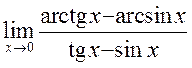 , 28)
, 28) 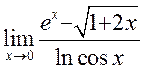 .
.
6. Производные и дифференциалы
1(!!). Определить значения α и β, при которых следующие функции
а) всюду непрерывны, б) всюду дифференцируемы:
1) 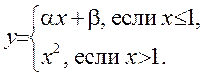 2)
2)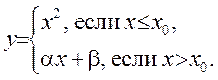 3)
3) 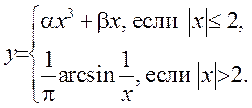
4)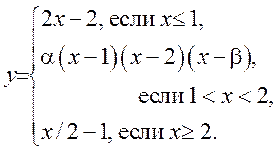
2(!). Исследовать на дифференцируемость:
1) 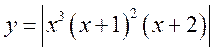 , 2)
, 2) ![]() .
.
3(!). Определить значения α и β, при которых функция К13.178
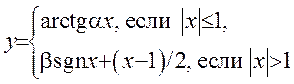 имеет производную: 1) в точке x=1, 2) в точке x=–1.
имеет производную: 1) в точке x=1, 2) в точке x=–1.
4. Найти правую и левую производные следующих функций. Определить, является ли функция дифференцируемой?
1)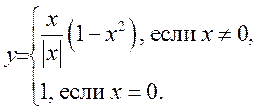 2)
2) 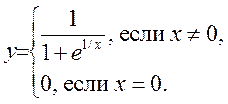 3)
3) 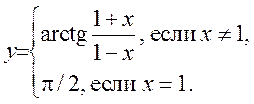
5. Найти ![]() ,
, ![]() и
и ![]() ,
, ![]() для функций, заданных параметрически: К13.201
для функций, заданных параметрически: К13.201
1)![]() , 2)
, 2) ![]() , 3)
, 3)![]() ,
,
4) ![]() .
.
6. Найти производные обратных функций в указанных точках К13.197
1)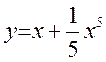 , а)
, а) ![]() , б)
, б) 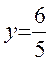 ;
;
2)![]() ;
;
3)![]() .
.
7. Вычислить ![]() .
.
К13.2087 В с.125N68
1)![]()
![]() ;
;
2) ![]() ,
, 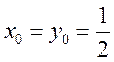 .
.
8. Найти ![]() для дифференцируемых функций
для дифференцируемых функций ![]() , заданных неявно:
, заданных неявно:
1)![]() , 2)
, 2)![]() .
.
9. Найти ![]() для дифференцируемых функций
для дифференцируемых функций ![]() , заданных неявно:
, заданных неявно:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() .
.
10(!!!).Сделать указанную замену переменных в уравнении:
1) ![]() В
с.125 N69
В
с.125 N69 ![]() ;
;
2) 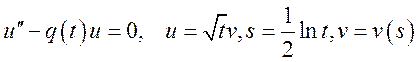 В с.125 N74
В с.125 N74 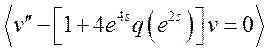 ;
;
3) 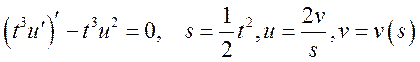 В с.125 N75
В с.125 N75 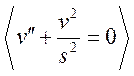 ;
;
4) 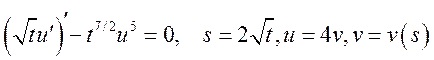 В
с.125 N76
В
с.125 N76 ![]() ;
;
5) ![]() В
с.125 N77
В
с.125 N77 ![]() .
.
11. Найти дифференциал функции y, считая известными дифференциалы функций u и v:
1)![]() ; 2)
; 2)![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5)![]() ; 6)
; 6) ![]() .
.
12(!!). Найти второй
дифференциал функции ![]() :
:
1) ![]() , 2)
, 2)![]() , 3)
, 3)![]() ,
,
4) ![]() , 5)
, 5) ![]() , 6)
, 6) ![]() , 7)
, 7) ![]() .
.
13(!!). Пользуясь теоремой Лагранжа, доказать неравенства:
1) ![]() ; 2)
; 2) ![]() ;
;
3) 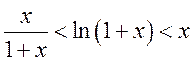 , при
, при
![]() ; 4)
; 4) 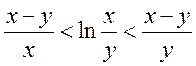 при
при ![]() ;
;
7) ![]() , при
, при ![]() ; 8)
; 8) ![]() , при
, при ![]() ;
;
9) ![]() ,
,![]() ;
;
10) ![]() ;
11)
;
11) ![]() ;
;
12) ![]() ;
13)
;
13) 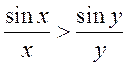 ,
, ![]() ;
;
14)![]() ;
;![]() .
.
7. Интегралы
1. Найти интеграл с переменным верхним пределом:
1) 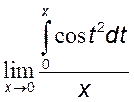 , 2)
, 2) 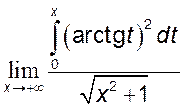 .
.
2. Доказать, что 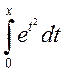 ~
~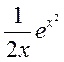 .
.
3. С помощью теоремы о среднем:
- определить знаки следующих определенных интегралов:
1) 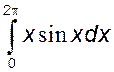 , 2)
, 2) 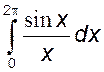 , 3)
, 3) 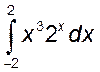 , 3)
, 3)
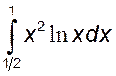 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.