13. Кратные интегралы
Замечание: особое внимание уделить цилиндрическим, сферическим, полярным системам координат. В билетах, предположительно, задачи на кратное интегрирование будут встречаться, в рамках задач на теорию поля.
1. Записать интеграл 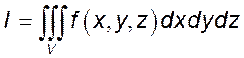 в
виде повторного или суммы повторных с указанным порядком интегрирования (если
указан порядок
в
виде повторного или суммы повторных с указанным порядком интегрирования (если
указан порядок ![]() , то требуется расставить пределы
интегрирования в следующем повторном интеграле
, то требуется расставить пределы
интегрирования в следующем повторном интеграле 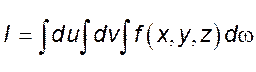 )
)
1. Область ![]() ограничена поверхностями
ограничена поверхностями ![]() ,
, ![]() , а)
, а) ![]() ,
,
б) ![]() .
.
2. Область ![]() ограничена поверхностями
ограничена поверхностями ![]() ,
, ![]() , а)
, а)![]() ,
,
б)![]() .
.
3. ![]() , а)
, а) ![]() , б)
, б) ![]() .
.
2. Свести интеграл к однократному или сумме однократных:
1. 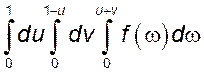 .
.
2. 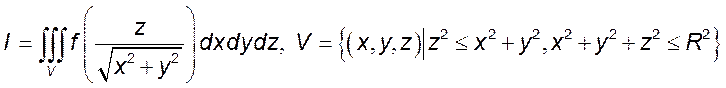 .
.
3. В интеграле 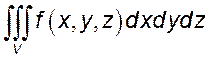 перейти к сферическим
координатам и записать его в виде повторного, если
перейти к сферическим
координатам и записать его в виде повторного, если
1) ![]() .
.
2) Область ![]() ограничена
поверхностями
ограничена
поверхностями ![]() .
.
4. Вычислить интеграл:
1) 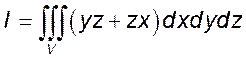 , область
, область ![]() расположена в первом октанте и ограничена
поверхностями
расположена в первом октанте и ограничена
поверхностями ![]() .
.
2) 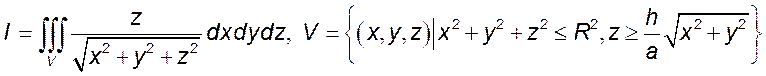 .
.
5. Вычислить площадь области, ограниченной кривой:
1) ![]() 2)
2) 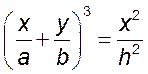 .
.
6. Найти объем тела, ограниченного поверхностью:
1) ![]() 2)
2) ![]() .
.
14. Теория поля
1. Найти работу поля ![]() вдоль
прямой от точки
вдоль
прямой от точки ![]() до точки
до точки ![]() ,
если:
,
если:
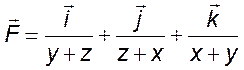 ,
, ![]() ,
, ![]()
2. Найти работу поля ![]() вдоль
кривой
вдоль
кривой ![]() , если:
, если:
1) ![]() ;
; ![]() – часть
графика
– часть
графика ![]() от точки
от точки ![]() до
точки
до
точки ![]()
2) ![]() ;
; ![]() -дуга
астроиды
-дуга
астроиды ![]() от точки
от точки ![]() до
точки
до
точки ![]() , расположенная в первом квадранте (
, расположенная в первом квадранте (![]() -непрерывная функция) [К12.92.3].
-непрерывная функция) [К12.92.3].
3) ![]() и
и ![]() есть
наименьшая дуга окружности
есть
наименьшая дуга окружности ![]() от точки
от точки![]() до точки
до точки ![]() [В178].
[В178].
4) ![]() – кратчайшая дуга эллипса
– кратчайшая дуга эллипса ![]() ,
, ![]() от точки
от точки![]() до точки
до точки ![]() : б)
: б)
![]() , в)
, в) ![]() .
.
3. Найти по формуле Стокса циркуляцию поля ![]() вдоль контура
вдоль контура ![]() , ориентированного
по часовой стрелке при взгляде на него из начала координат, если:
, ориентированного
по часовой стрелке при взгляде на него из начала координат, если:
![]() ,
, ![]() .
.
4. Найти циркуляцию вектора ![]() вдоль
ориентированного контура
вдоль
ориентированного контура ![]() .
.
1) ![]() ,
, ![]() положительно
ориентированная на правой стороне плоскости.
положительно
ориентированная на правой стороне плоскости.
2) ![]() ,
,
![]() , положительно ориентированная на внешней
стороне параболоида.
, положительно ориентированная на внешней
стороне параболоида.
5. Найти поток векторного поля ![]() через
поверхность
через
поверхность ![]() в направлении внешней нормали
в направлении внешней нормали
1) ![]() ,
,
![]() .
.
2) ![]() ,
,
![]() – поверхность тела
– поверхность тела ![]() .
.
3) ![]() ,
,
![]() – верхняя сторона треугольника
– верхняя сторона треугольника ![]() , где
, где ![]() ,
, ![]() ,
, ![]() .
.
4) ![]() ,
,
![]() – поверхность пирамиды, образуемой
плоскостью
– поверхность пирамиды, образуемой
плоскостью ![]() и координатными плоскостями.
и координатными плоскостями.
5) ![]() ,
,
![]() – ограниченная часть параболоида
– ограниченная часть параболоида ![]() , отсеченная плоскостью
, отсеченная плоскостью ![]() .
.
6) ![]() ,
,
![]() – часть сферы
– часть сферы ![]() ,
расположенная в области
,
расположенная в области ![]() .
.
6. Найти дивергенцию поля 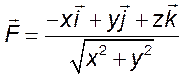 в
точке
в
точке ![]() . Чему приближенно равен поток вектора
. Чему приближенно равен поток вектора ![]() через бесконечно малую сферу
через бесконечно малую сферу ![]() ?
?
7. Дано векторное поле 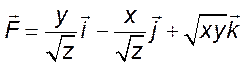 .
Вычислив
.
Вычислив ![]() в точке
в точке ![]() , приближенно
найти циркуляцию поля вдоль бесконечно малой окружности
, приближенно
найти циркуляцию поля вдоль бесконечно малой окружности
![]() ,
, ![]() ,
,
где ![]() .
.
15. Интегралы, зависящие от параметра
Замечание: знать алгоритм полного анализа ряда/интеграла на равномерную/абсолютную сходимость. Уметь использовать признаки Дирихле, Абеля, Вейерштрасса и теорему о сходимости.
1. Доказать равномерную сходимость на указанном интервале
1) 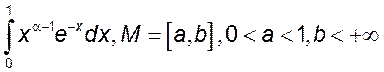 , 2)
, 2) 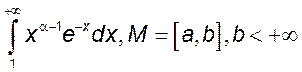 ,
,
3) 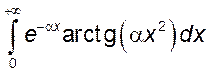 , а)
, а) ![]() , 4)
, 4) 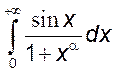 ,
, ![]() .
.
2. Исследовать на равномерную сходимость на указанном множестве
1)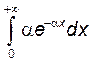 , а)
, а)![]() ,
б)
,
б)![]() .
.
2)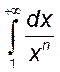 , а)
, а)![]() , б)
, б)![]() .
.
3) 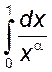 ,
, ![]() . 4)
. 4)
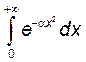 , а)
, а) ![]() , б)
, б) ![]() .
.
5) 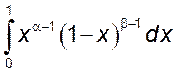
![]() . 6)
. 6) 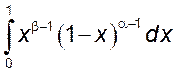
![]() . 7)
. 7)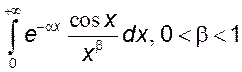 ,
,![]() . 8)
. 8)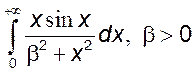 ,
,![]() .
.
3. Найти:
1) 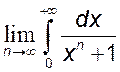 . 2)
. 2) 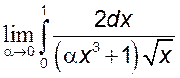 3)
3) 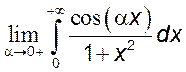 .
.
4. Исследовать на непрерывность в указанном множестве ![]() следующую функцию
следующую функцию ![]()
1) 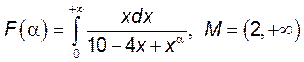 . 2)
. 2) 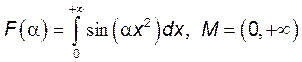 .
.
3) 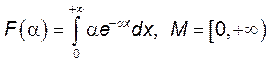 . 4)
. 4)
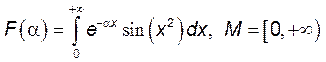 .
.
5. Найти производную функции ![]() :
:
1) 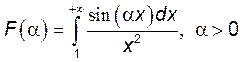 . 2)
. 2) 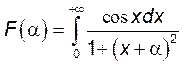 .
.
Старший составитель: доц. С.Е. Рояк
Младшие составители/Оформители: Койфман Дмитрий (ПМ-12),
Сорокин Александр (ПМ-12).
* усложненный номер (возможно, именно на эти номера следует обратить внимание – а не решать все подряд?!)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.