- определить, какой интеграл больше: 1) 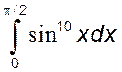 или
или 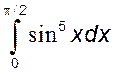 ,
,
2) 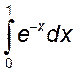 или
или 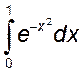 , 3)
, 3) 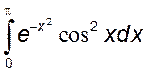 или
или 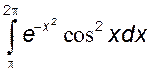 .
.
- оценить интеграл
1) 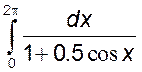 , 2)
, 2) 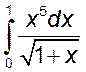 , 3)
, 3) 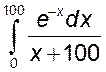 .
.
4. Найти площадь области, ограниченной кривой, заданной
параметрически ![]() .
.
5. Найти площадь области, ограниченной кривой, заданной в полярных координатах:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4)
![]() ,
,
5) ![]() , 6)
, 6) ![]() , 7)
, 7)
![]() , 8)
, 8) ![]() ,
,
9) *![]() , 10) *
, 10) *![]() .
.
6. Вычислить площадь, описываемую полярным радиусом спирали
Архимеда ![]() при одном его обороте, если началу
движения соответствует
при одном его обороте, если началу
движения соответствует ![]() .
.
7. Найти площадь фигуры, ограниченной улиткой Паскаля ![]() .
.
8. Найти длину дуги кривой:
1) ![]() , 2)
, 2) 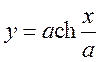 от точки
от точки ![]() до
точки
до
точки ![]() ,
,
3) ![]() , 4)
, 4) ![]() ,
,
5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() ,
,
8) ![]() , 9)*
, 9)* 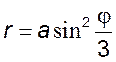 , 10)
, 10)
![]() .
.
9. Исследовать сходимости интегралов от неотрицательных функций:
1) 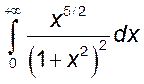 , 2)
, 2)
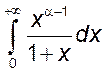 , 3)
, 3) 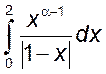 , 4)
, 4) 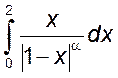 , 5)
, 5) 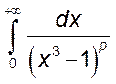 ,
,
6) 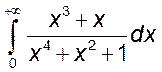 , 7)
, 7) 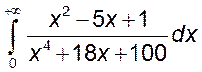 , 8)
, 8) 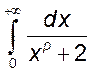 , 9)
, 9) 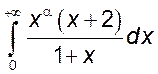 ,
,
10) 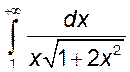 , 11)
, 11) 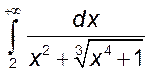 , 12)
, 12) 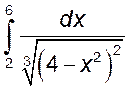 , 13)
, 13) 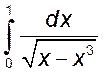 ,
,
14) 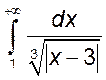 , 15)
, 15) 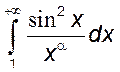 , 16)
, 16) 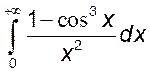 , 17)
, 17) 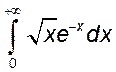 ,
,
18) 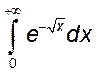 , 19)
, 19) 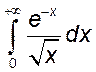 , 20)
, 20) 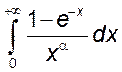 ,
,
21)* 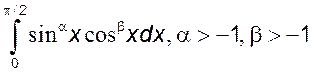 ,
,
22) 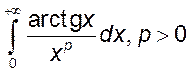 , 23)
, 23) 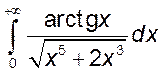 , (24)*
, (24)*
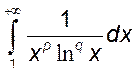 ), 25)
), 25)
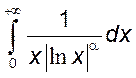 ,
,
26) 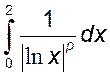 , 27)
, 27) 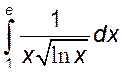 , 28)*
, 28)* 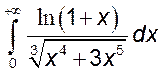 , 29)*
, 29)*
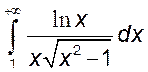 .*
.*
10. Исследовать интегралы на абсолютную и условную сходимость:
1) 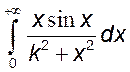 , 2)
, 2) 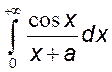 , 3)
, 3) 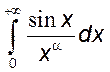 , 4)
, 4)
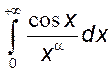 ,
,
5) 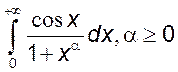 , 6)
, 6) 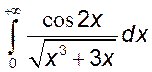 , 7)
, 7) 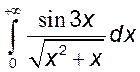 , 8)
, 8)
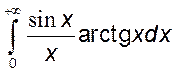 ,
,
9)* 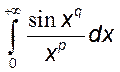 , 10)
, 10) 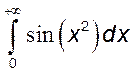 , 11)
, 11) 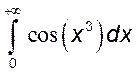 , 12)*
, 12)*
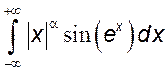 ,
,
13)* 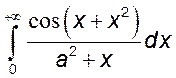 , 14)*
, 14)* 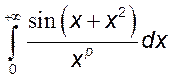 , 15)*
, 15)* 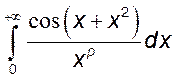 .
.
8. Предел и непрерывность функций многих переменных
Замечание: не забывайте правильно выбирать систему координат: декартовую/полярную!
В номерах этого раздела ошибка может оказаться роковой!!
1. Найти а) ![]() ,
б)
,
б) ![]() , в)
, в) 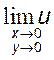 .
.
1) 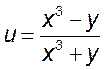 , 2)
, 2) 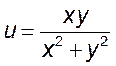 , 3)
, 3) 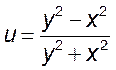 .
.
2. Найти а) ![]() ,
б)
,
б) ![]() , в)
, в) 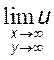 .
.
1) 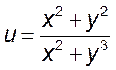 , 2)
, 2) 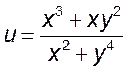 , 3)
, 3) 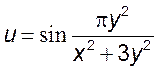 .
.
3. Найти:
1)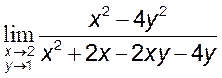 , [1] 2)
, [1] 2)
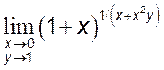 ,[e] 3)
,[e] 3)
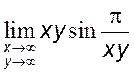 , [p]
, [p]
4) 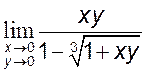 , [-3] 5)
, [-3] 5) 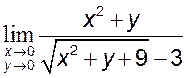 , [6] 6)
, [6] 6)
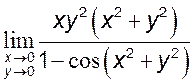 , [0]
, [0]
7) 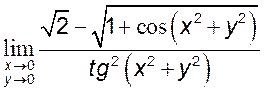 , [
, [![]() ] 8)
] 8)
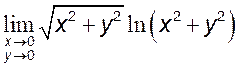 , [0]
, [0]
9) 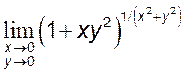 , [1] 10)
, [1] 10) 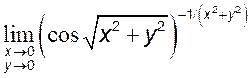 .
.
4. Доказать, что следующие функции непрерывны в начале координат:
1) 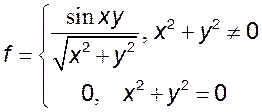 2)
2) 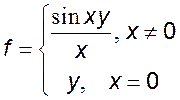 3)
3) 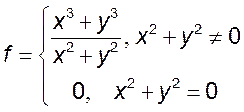
4) 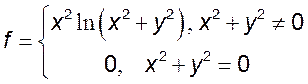 5)
5) 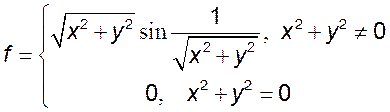 6)
6)![]()
5. Найти точки разрыва следующих функций:
1) 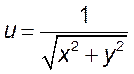 , 2)
, 2) 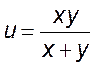 , 3)
, 3) 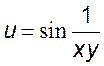 ,
4)
,
4) 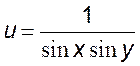 .
.
6. Доказать, что следующие функции не являются непрерывными в начале координат:
1)* 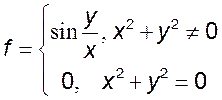 2)
2) 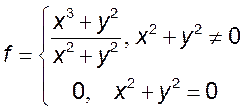
3) 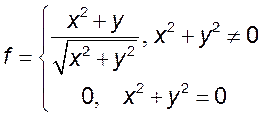 4)
4)
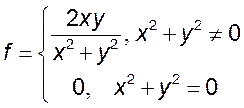
7. Выяснить, является ли функция 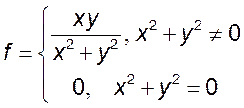 в
точке (0,0):
в
точке (0,0):
1) непрерывной по x, 2) непрерывной по y, 3) непрерывной.
8. Найти значение a, при
котором функция 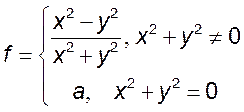 в точке (0,0) является: 1)
непрерывной по x, 2) непрерывной по y, 3) непрерывной по кривой
в точке (0,0) является: 1)
непрерывной по x, 2) непрерывной по y, 3) непрерывной по кривой ![]() ,
,
4) непрерывной.
9. Найти значение a, при
котором функция 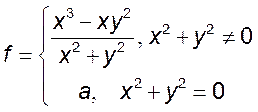 в точке (0,0) является: 1)
непрерывной по прямой
в точке (0,0) является: 1)
непрерывной по прямой ![]() , 2) непрерывной.
, 2) непрерывной.
10. Найти значение a, при
котором функция 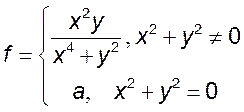 в точке (0,0) является: 1)
непрерывной по прямой
в точке (0,0) является: 1)
непрерывной по прямой ![]() , 2) непрерывной по кривой
, 2) непрерывной по кривой ![]() , 3) непрерывной.
, 3) непрерывной.
11. Найти все точки разрыва, указать точки устранимого разрыва функции двух переменных:
1) 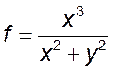 , 2)
, 2)
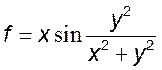 ,
3)*
,
3)* 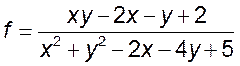 ,
,
6) 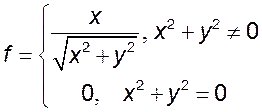 7)
7) 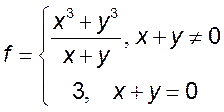 8)
8) 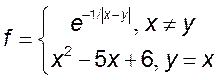
12. Найти все точки разрыва функции трех переменных:
1) 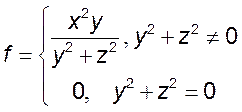 2)
2) 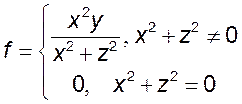 3)
3)
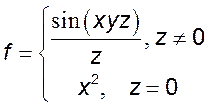
4) 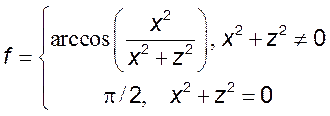 5)
5) 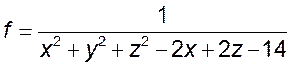 6)
6) ![]()
7) 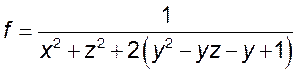 8)
8) ![]() .
.
9. Производные и дифференциалы высших порядков:
1. А) Выписать все ненулевые дифференциалы функции.
Б) Найти ![]() в
точке
в
точке ![]() .
.
В) Найти производную функции f в точке ![]() по направлению вектора
по направлению вектора ![]() ,
,
![]() ,
, ![]() .
.
1) ![]() , 2)
, 2) ![]() ,
,
3) ![]() , 4)
, 4) ![]() ,
,
5) ![]() , 6)
, 6) ![]() .
.
2. Найти ![]()
1) ![]() , 2)
, 2) ![]() ,
,
3. Найти частные производные первого порядка функции ![]() , заданной неявно, предварительно найдя ее
первый дифференциал:
, заданной неявно, предварительно найдя ее
первый дифференциал:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.