1) ![]() , 2)
, 2) 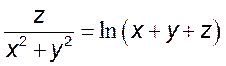 , 3)
, 3)
![]()
4. Найти первый и второй дифференциалы функций ![]() , заданных неявно:
, заданных неявно:
1) ![]() ,
2)
,
2) ![]()
5. Найти второй дифференциал в точке ![]() ,
,
![]() функции
функции ![]() , заданной
неявно, если:
, заданной
неявно, если:
1) ![]() ,
2)
,
2) ![]() .
.
6. Найти дифференциалы первых двух порядков сложной функции u, если ![]() дважды непрерывно
дифференцируемая функция и
дважды непрерывно
дифференцируемая функция и ![]() независимые переменные
независимые переменные
1) ![]() ,
,
2) ![]() , 3)
, 3) ![]() ,
,
4) ![]() , 5)
, 5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() ,
,
8) ![]() , 9)
, 9) ![]()
7. Проверить, что данное уравнение однозначно определяет
функцию ![]() в окрестности точки
в окрестности точки ![]() : 1)
: 1) ![]() , 2)
, 2)
![]() .
.
Замечание: связать с равенством нулю частной производной.
8. Проверить, что данное уравнение однозначно определяет
функцию ![]() в окрестности точки
в окрестности точки ![]() :
: ![]() .
.
9(!!). Сделать замену переменных:
1)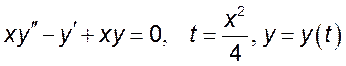 , 2)
, 2) 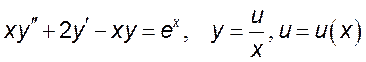 ,
,
3)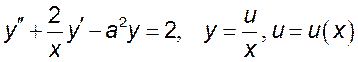 ,
4)
,
4)![]() ,
,
5)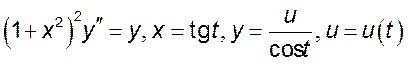 ,
6)
,
6)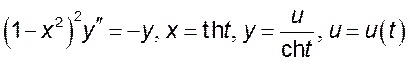 ,
,
7)![]() 8)
8)
![]() .
.
10. Приняв u и v за новые независимые переменные, преобразовать следующие уравнения:
1) 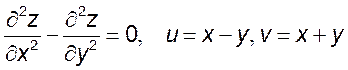 , 2)
, 2) 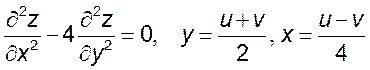 ,
,
3) 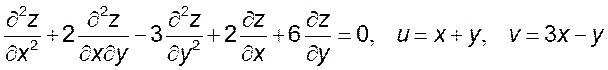 .
.
11. Приняв u, v и w за новые независимые переменные, преобразовать следующие уравнения:
1) 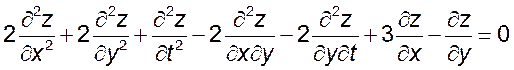 ,
, ![]() ,
,
2)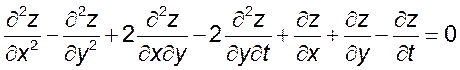 ,
, ![]() .
.
12. Приняв u и v за новые независимые переменные, а w за новую функцию от u и v, преобразовать к новым переменным следующие уравнения:
1) 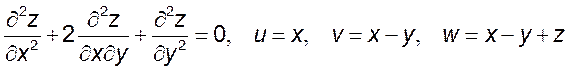 ,
,
2) 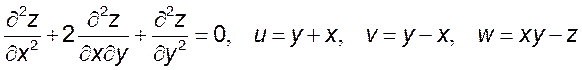 .
.
10(!!!!). Экстремумы функций многих переменных
1. Исследовать функцию u на экстремум
1)![]() 7)
7)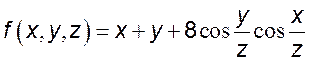
2)![]() 8)
8)
![]()
3)![]() 9)
9)
![]()
4)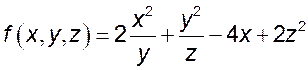 10)
10)![]()
5)![]() 11)
11)
![]()
6)![]() 12)
12)
![]()
2. Исследовать на экстремум непрерывно дифференцируемую
функцию ![]() , заданную неявно: 1)
, заданную неявно: 1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
![]()
3. Исследовать на экстремум непрерывно дифференцируемую
функцию ![]() , заданную неявно:
, заданную неявно:
1) ![]() 5)
5)![]()
2) ![]() 6)
6)
![]()
3) ![]() 7)
7)
![]()
4) ![]() 8)
8)![]()
4.Исследовать на экстремум непрерывно дифференцируемую
функцию ![]() , заданную неявно: 1)
, заданную неявно: 1) ![]()
2) ![]() 3)
3)
![]() .
.
5. Найти условные экстремумы функции ![]() относительно
заданного уравнения связи: 1)
относительно
заданного уравнения связи: 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() ,
,
4) 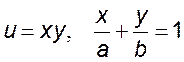 , 5)
, 5) 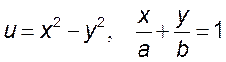 , 6)
, 6) 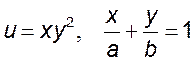 , 7)
, 7)![]() , 8)
, 8) ![]() ,
,
9) ![]() ,
,
6. Найти условные экстремумы функции ![]() при
заданных уравнениях связи:
при
заданных уравнениях связи:
1) ![]() , 2)
, 2) ![]() ,
,
3) ![]() , 4)
, 4) ![]() ,
,
5) ![]() , 6)
, 6) ![]() ,
,
7) ![]() .
.
7. Найти наибольшее и наименьшее значения функции в заданной области:
1) ![]() , 2)
, 2) ![]() ,
,
3) ![]() , 4)
, 4) ![]() ,
,
4) ![]() , 5)
, 5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() ,
,
8) ![]() , 9)
, 9) ![]() ,
,
10) ![]() , 11)*
, 11)* ![]() ,
,
12) ![]() ,
,
13)* ![]() ,
,
14)* ![]() .
.
11. Функциональные последовательности и ряды
1. Найти предельную функцию последовательности
1. 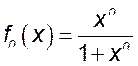 , 2.
, 2.
![]()
2. Исследовать на равномерную сходимость последовательность
на множестве ![]()
1. ![]() , а)
, а) ![]() , б)
, б) ![]() .
.
2. ![]() , а)
, а) ![]() , б)
, б) ![]() .
.
3. 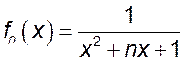 , а)
, а) ![]() , б)
, б) ![]() .
.
3(!). Исследовать сходимость функциональный ряд:
1. 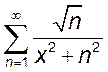 , 2.
, 2.
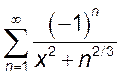 , 3.
, 3. 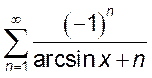 ,
4.
,
4. 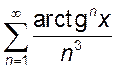
4(!). Исследовать на равномерную сходимость ряд на
множестве ![]() :
:
1. 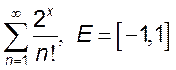 ; 2.
; 2. 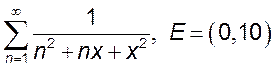 ;
;
3. 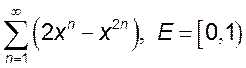 ; 4.
; 4.
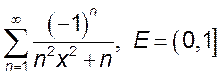 .
.
5(!). Исследовать на равномерную сходимость ряд:
1. 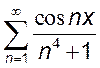 ; 2.
; 2.
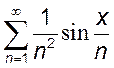 ;
;
3. 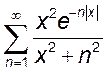 ; 4.
; 4.
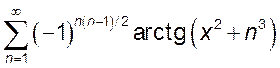 .
.
12. Степенные ряды
Замечание: кто забудет про радиус сходимости, тому – …!
1(!!). Найти множество сходимости ряда
1. 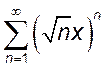 , 2.
, 2. 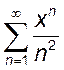 , 3.
, 3. 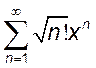 , 4.
, 4.
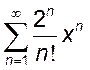 , 5.
, 5. 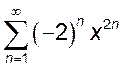 .
.
2(!!). Разложить функцию ![]() в
степенной ряд с центром в точке
в
степенной ряд с центром в точке ![]() . Указать радиус
сходимости полученного ряда:
. Указать радиус
сходимости полученного ряда:
1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. 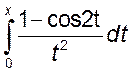 ;
;
4. ![]() ; 5.
; 5. 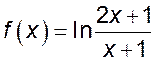 ;
;
6. 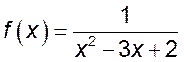 ; 7(!!!).
; 7(!!!).
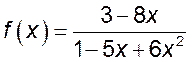 .
.
3. Разложить функцию ![]() в
степенной ряд с центром в указанной точке
в
степенной ряд с центром в указанной точке ![]() .
Указать радиус сходимости полученного ряда.
.
Указать радиус сходимости полученного ряда.
1. ![]() а)
а) ![]() , б)
, б) ![]() ; 2.
; 2. ![]() ,
, ![]() ;
;
3. ![]() , а)
, а) ![]() , б)
, б) ![]() ; 4.
; 4. 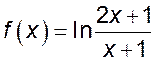 ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.