Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 9

Так как , то можно записать:

                                                                                                              (4.8)    

Так как , то 

                         (4.9)

График импульсной характеристики цепи представлен на рисунке 4.2.

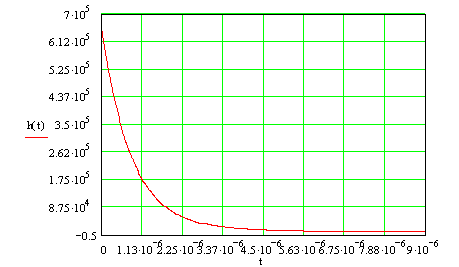
Рисунок 4.2- График импульсной характеристики цепи.

5. Спектр выходного сигнала

5.1 Спектральная плотность выходного сигнала

         Спектральный анализ выходного сигнала аналогичен спектральному анализу входного сигнала. Найдём сначала спектральную плотность выходного сигнала, а затем амплитудный и фазовый спектры выходного сигнала.

Спектральная плотность имеет вид:

.                                           (5.1)

Подставив (2.4) и (3.14) в (5.1), получим:

(5.2)

Заменим оператор  на  и воспользовавшись результатом пункта 2.1. запишем:

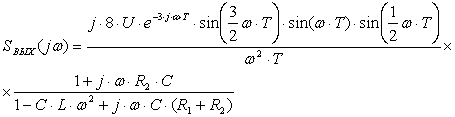.           (5.3)

5.2 Амплитудный и фазовый спектры выходного сигнала

Амплитудный спектр выходного сигнала есть модуль спектральной плотности . Согласно (5.3) получим:

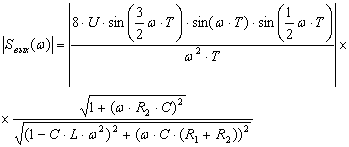.                       (5.4)

График амплитудного спектра приведён на рисунке 5.1.

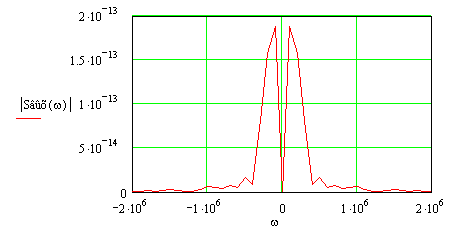
Рисунок 5.1 – Амплитудный спектр выходного сигнала

Фазовый спектр выходного сигнала есть аргумент спектральной плотности

Для  получим:

,(5.5)

Если  тогда:

,(5.6)

График фазового спектра приведён на рисунке 5.2.

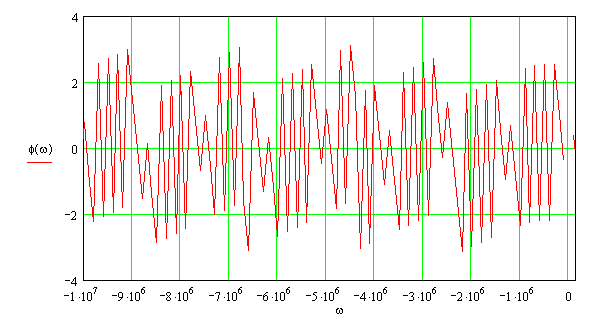
Рисунок 5.2 – Фазовый спектр выходного сигнала

5.3 Определение ширины спектра выходного сигнала

Ширина спектра выходного сигнала определится из рисунка (5.3). Проводится уровень 0,1 от максимального значения и определяется последнее пересечение графика с этим уровнем. Считая, что ширина спектра равна целому числу полуволн, находим  :

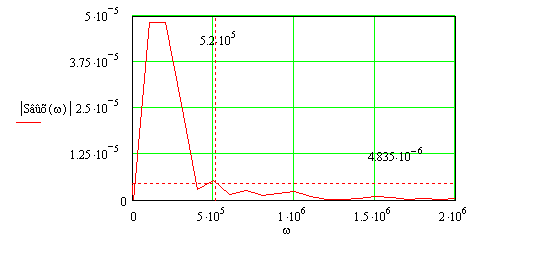
Рисунок 5.3 – Определение ширины спектра выходного сигнала

 

6. Выходной сигнал

Запишем выходной сигнал в операторной форме:

.                                   (6.1) 

Подставим в (6.1) соответствующие выражения для  и .

(6.2)