Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 3

1. Корреляционная функция входного сигнала

Входной сигнал:

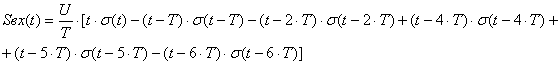
Для детерминированного сигнала S(t) конечной длительности корреляционная функция определяется так:

,                                        (1.1)

где  - величина временного сдвига сигнала.

Корреляционная функция характеризует степень связи сигнала S(t) с его копией, сдвинутой на величину   по оси времени.

Функция  достигает максимума при , так как любой сигнал полностью коррелирован с самим собой.

,                                   (1.2) 

Максимальное значение корреляционной функции равно энергии сигнала.

Наряду с выражением (1.1) верно равенство (1.3).

.                               3)     

Т.е.  является четной функцией .

График входного сигнала представлен на рисунке (1.1)

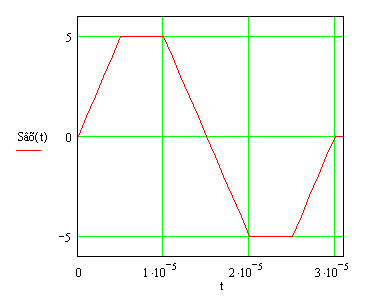
Рисунок 1.1 График входного сигнала

На рисунках  (1.2), (1.3), (1.4), (1.5), (1.6), (1.7) изображен сигнал . На нём  же представлена его “копия”, сдвинутая во времени в сторону запаздывания на  с. Произведение  отлично от нуля лишь в пределах интервала времени, когда наблюдается наложение сигналов. Зная, что корреляционная функция четна, рассмотрим ее на интервале .

1.1 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

Рисунок 1.2 – Графики входного сигнала  и сдвинутого во времени сигнала  при

Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующей цепочкой интегралов:

        

.                (1.4)

В результате вычислений получим:

 

Подставим численные значения:

,

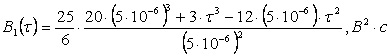получим:

1.2 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

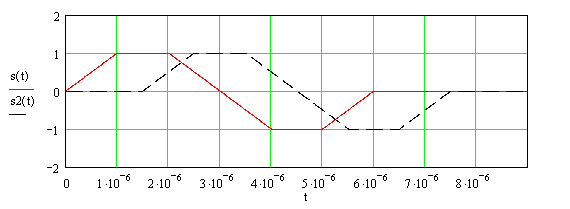
Рисунок 1.3 –  Графики входного сигнала  и сдвинутого во времени сигнала  при