Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 5

Подставим численные значения:

,

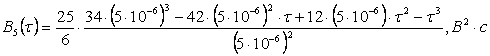получим:

1.6 Нахождение корреляционной функции для входного сигнала, сдвинутого на  при 

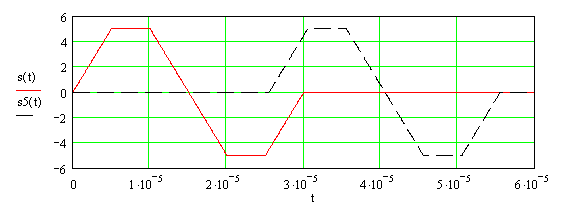
Рисунок 1.7 – Графики входного сигнала  и сдвинутого во времени сигнала  при

Корреляционная функция для входного сигнала, сдвинутого на , при  определяется следующим интегралом:

.                           (1.10)

В результате вычислений получим:

.

Подставим численные значения:

,

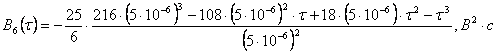получим:

1.7 Построение графика корреляционной функции для входного сигнала

Выражение для корреляционной функции на интервале  при помощи функции включения  будет иметь вид:

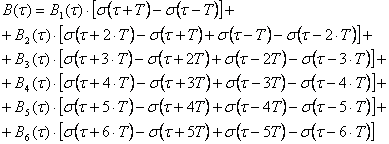.               (1.11)        

График корреляционной функции представлен на рисунке 1.8.

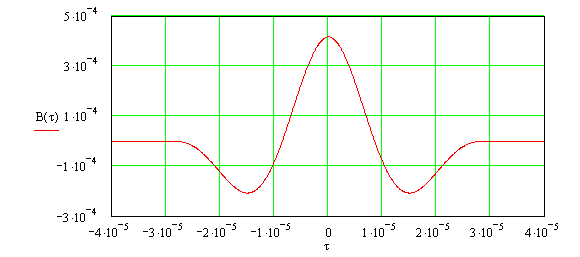
Рисунок 1.7 – Корреляционная функция входного сигнала

1.8 Нахождение интервала корреляции

Интервал корреляции определится по формуле (1.11):

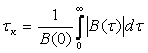                                            (1.12)        

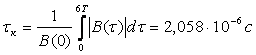
2 Спектральный анализ входного сигнала

2.1 Спектральная плотность входного сигнала

Целью спектрального анализа является выявление амплитудного и фазового спектров сигнала. Их можно найти из выражения для спектральной плотности:

модуль этого выражения представляет собой амплитудный спектр, а аргумент – фазовый спектр. Поэтому найдём выражение для спектральной плотности.

Представим входной сигнал  через функцию включения:

.                       (2.1)

Запишем сигнал в операторной форме, используя формулу перехода к операторной форме (2.2) и свойство временного сдвига (2.3):

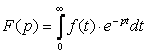,                                                     (2.2)

.                                        (2.3)        

С учетом преобразований Лапласа слагаемые выражения (2.1) будут иметь вид:

1) ,

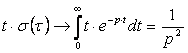2) ,

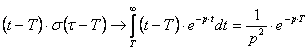3) ,

         4) ,

5) ,