Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 10

Обозначим выражение

.                  (6.3) 

Воспользуемся результатами пункта 4.1.

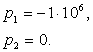
 - полюсы второго порядка.

,                               (6.4)

Найдем вычеты в точках , где

.

Найдём вычеты для первого корня:

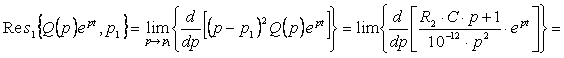
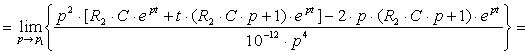
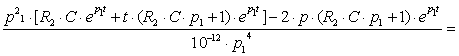
                         (6.5)

Найдём вычеты для второго корня:

              

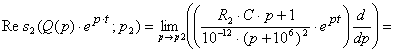
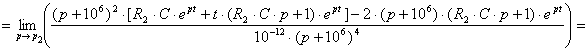
                                                                   (6.6)

Функция  будет определяться как сумма вычетов.

.                                   (6.7)

На основе временного сдвига для преобразований Лапласа

выходной сигнал примет вид:

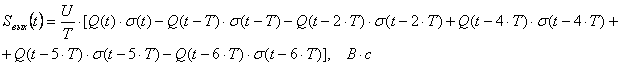  (6.8)   

         График выходного сигнала представлен на рисунке 6.1

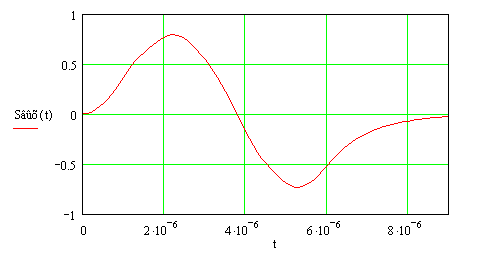
Рисунок 6.1 – Выходной сигнал

6 Выходной сигнал

Известно, что выходной сигнал в операторной форме выглядит следующим образом:

        (6.1)

тогда              

                    (6.2)

Рассмотрим функцию:

                 (6.3)

С помощью теории вычетов, найдем оригинал этой функции:

 Разложим знаменатель этой функции на произведение нескольких функций:

              (6.4)

Найдем корни знаменателя функции W(p):

Теперь найдем вычеты для полюсов 2-ого порядка:

1)Для  

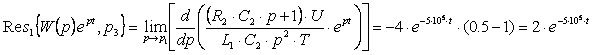 (6.5)

2) Для ,

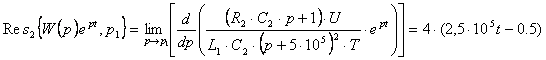           (6.6)

Так как , то                                 

                                           (6.7)

Мы знаем, что

                                          (6.8)

Тогда, зная оригинал функции W(p), находим :

раскрываем скобки в уравнении 6.8. На основе свойства временного сдвига для преобразований Лапласа