Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 7

3 Частотный коэффициент передачи цепи

3.1 Коэффициент передачи цепи

Исходная схема представлена на рисунке 3.1.

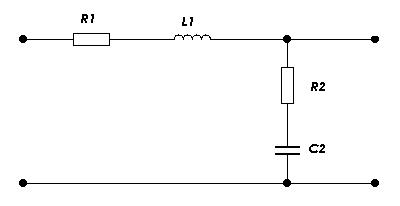
Рисунок 3.1  : Исходная схема.

Представим схему в операторной форме. Исходная схема в операторной форме представлена на рисунке 3.2.

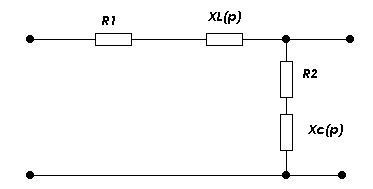
Рисунок 3.2 : Исходная схема в операторной форме.

Где:

                                            

                                 

Преобразуем цепь, как показано на рисунке 3.3:

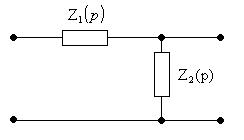
Рисунок 3.3: Исходная цепь в операторной форме после преобразования

Здесь:

                                                    

                                          

Анализ прохождения сигнала через линейную цепь и преобразования в ней спектра сигнала основан на использовании амплитудно-частотной и фазочастотной характеристик цепи. Амплитудно-частотная и фазочастотная характеристики представляют собой соответственно модуль и аргумент комплексного коэффициента передачи цепи K(ω).

В операторной  форме комплексный коэффициент передачи выражается:

                                                                           (3.1)

где

                                                             

  , тогда

                                             

                               

                                                      

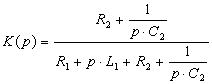                                                             (3.2)

Преобразовав K(p), получим:

                                                     (3.3)

Перейдем к комплексной форме заменив, оператор p на jω:

                                         (3.4)

3.2 Амплитудно-частотная и фазочастотная характеристики цепи

Амплитудно-частотная характеристика цепипредставляет собоймодуль

комплексного коэффициента передачи цепи .

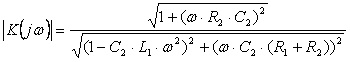             (3.5)

Подставив исходные параметры элементов цепи, строим график амплитудно-частотной характеристики цепи.

График амплитудно-частотной характеристики цепи представлена на рисунке 3.4.

Рисунок 3.4:  График амплитудно-частотной характеристики цепи.

Фазочастотная характеристика цепи представляет собой аргументкомплексного коэффициента передачи цепи .

Рассмотрим :

Значение аргументакомплексного коэффициента передачи цепи будет зависеть от знака .