Анализ прохождения детерминированного сигнала через линейную цепь с постоянными параметрами (пояснительная записка), страница 8

Рассмотрим уравнение:

                                                                              (3.6)

                                                       

                                                       

Подставив численные значения, найдем, :

Таким образом:

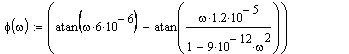        (3.7)

График фазочастотной характеристики цепи представлен на рисунке 3.5.

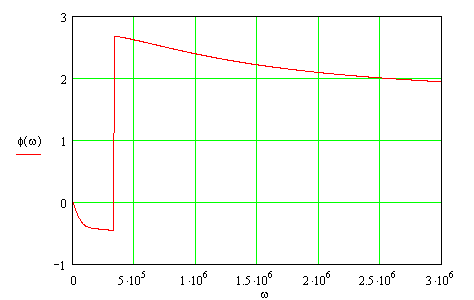
Рисунок 3.5: График фазочастотной характеристики цепи.

4. Импульсная и переходная характеристика цепи

4.1 Переходная характеристика цепи

Переходным процессом называется процесс характеризующийся переходом электрической цепи из одного электрически устойчивого состояния в другое, в течении некоторого времени.

Переходная характеристика цепи g(t) представляет собой реакцию цепи на выходе при воздействии на входе сигнала, описываемого единичной функцией.

Найдем  изображение переходной характеристики - g(p) , а затем при помощи вычетов найдем оригинал g(t).

Известно, что:

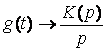                                                                                                 (4.1)

Представим g(p) в виде:

                        (4.2)

Подставляя K(p) в выражение для g(p) получим:

            (4.3)         

Для нахождения оригинала g(t), воспользуемся теорией вычетов.

Решим уравнение:

                              (4.4)

Решив 4.4, получим:

Знаменатель выражения (4.3) разложим на множители, тогда:

                        (4.5)

Найдём вычеты для корней знаменателя:

  1) Для :  

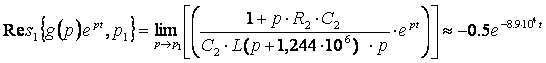
2) Для:

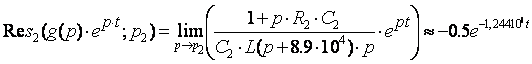
2) Для:

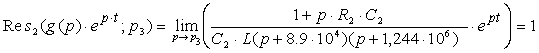
Функция g(t) будет определяться как сумма вычетов.

                                         (4.6)            

                                                                                (4.7)

График переходного процесса приведён на рисунке 4.1

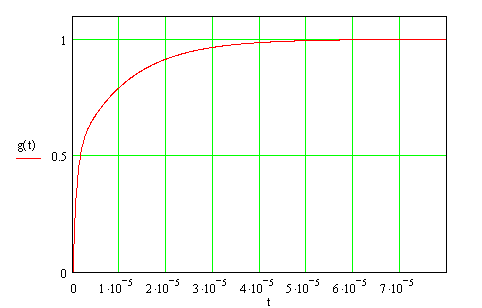
Рисунок 4.1: График переходного процесса.

4.2 Импульсная характеристика цепи.

Импульсной характеристикой цепи h(t) является реакция цепи на воздействие входного сигнала, который описывается  функцией.

Импульсной характеристикой цепи h(t) является реакция цепи на воздействие входного сигнала, который описывается  функцией.