













Глава 4
Метрологическое обеспечение робастных систем управления
С точки зрения надёжности функционирования робастные системы проектируются как распределённые. Степень сосредоточенности, при этом зависит только от сложности критерия управления технологическим процессом и сложности критериев оценки эффективности отдельных аппаратов и узлов. Метрологические характеристики, при этом, полностью определяются теоремами Ляпунова А.М.
|
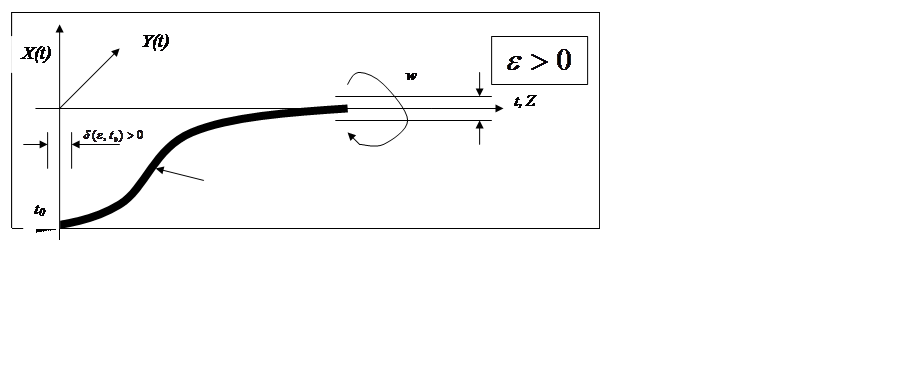
Рис. 4.1. Основные метрологические характеристики робастных систем
На
рисунке 4.1 представлена модельная траектория движения объекта управления с
пятимерной эталонной математической моделью. Пусть известно решение системы F (X,Y,Z,t,w) (на рисунке 4.1
жирная линия). Это решение будем называть программным (эталонным). Любое
отличие от этого эталонного движения будем называть возмущённым движением.
Тогда, невозмущенное движение F0(t) называется
устойчивым по Ляпунову, если для любого ![]() и любого числа
и любого числа ![]() можно указать число
можно указать число ![]() таким, что при норме разности:
таким, что при норме разности: ![]() будет выполняться условие:
будет выполняться условие: ![]() при
при ![]() , где
, где ![]() - это возмущенное движение, проходящее
через точку
- это возмущенное движение, проходящее
через точку ![]() в момент
в момент ![]() . Здесь
под нормой понимается:
. Здесь
под нормой понимается: 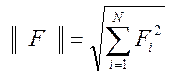 . При этом, если
коэффициенты эталонной модели дрейфуют случайным образом, то согласно второму
началу Ляпунова, невозмущенное
движение F0(t) называется
асимптотически устойчивым, а величину ∆0 для любого ∆ >0 можно выбрать
так, что (см. рис.4.2):
. При этом, если
коэффициенты эталонной модели дрейфуют случайным образом, то согласно второму
началу Ляпунова, невозмущенное
движение F0(t) называется
асимптотически устойчивым, а величину ∆0 для любого ∆ >0 можно выбрать
так, что (см. рис.4.2):
![]() .
.
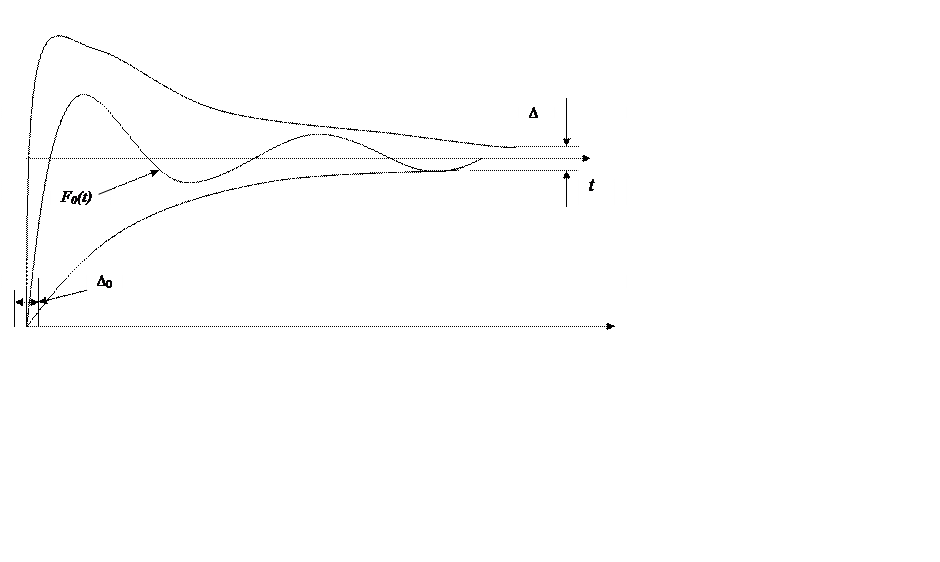
Рис. 4.2. Главная метрологическая характеристика робастной системы
Величину ∆0 будем называть случайной фазой начала движения [7]. Эта величина позволяет применить теорию потенциальной помехоустойчивости Котельникова А.В. [18] для описания метрологических характеристик переходных процессов в робастной системе адаптивного управления.
Поскольку алгоритмы управления содержат процедуры идентификации, требующие накопления информации, то быстродействие информационно-измерительной подсистемы (ИИС) должно быть приведено в соответствие с периодом нанесения управляющих воздействий, Ту, что практически осуществимо посредством оптимального выбора периода опроса первичных преобразователей, Тs.
Методическая динамическая погрешность всех измерительных каналов робастной системы обусловлена свойствами аналоговых элементов, влиянием внешних воздействий, отличием частотных спектров программно обрабатываемых сигналов от частотных спектров реальных измеряемых сигналов и от свойств цифровых элементов системы. Так как оптимальное управление, по своей структуре, напоминает систему автоматического регулирования и состоит из трех основных частей (объект управления, модуль идентификации математической модели объекта и алгоритма управления) структурную схему выделения погрешности можно представить так, как это изображено на рисунке 4.3. На рисунке: П(t)–помеха измерения критерия управления, hЭР(t)–весовая функция эталонного закона регулирования, hЭО(t)– эталонная модель объекта управления, hЭ(t)–весовая функция эталонной замкнутой системы, hРР(t)–весовая функция замкнутой робастной системы управления, Y(t)–текущие значения переходного процесса (критерия управления) эталонной системы регулирования, Z(t)– текущие значения виртуального прибора для измерения критерия управления, E(t)–ошибки цифровой обработки информации.
|
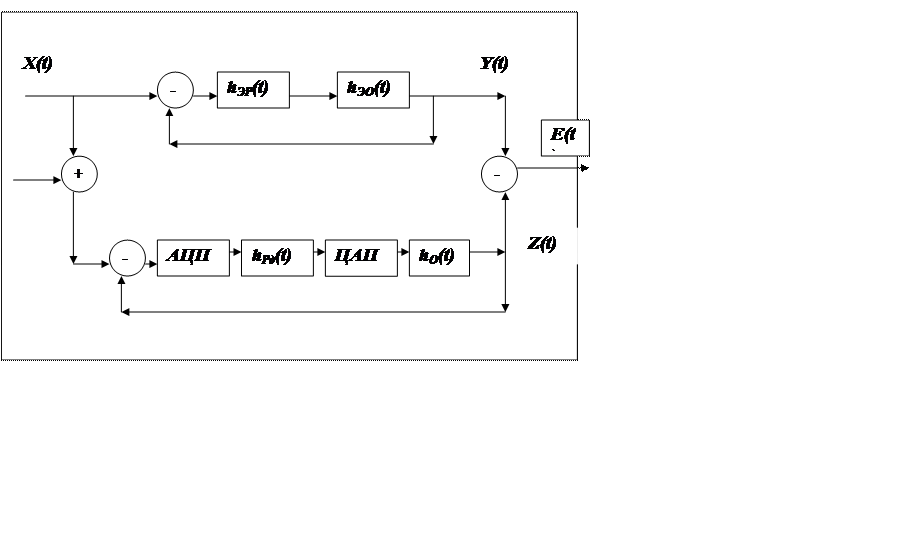
Рис. 4.3 – Схема выделения погрешности обработки информации в робастных системах управления
Из рисунка 4.3 видно, что
![]() и если записать автокорреляционную
функции эталонного переходного процесса как
и если записать автокорреляционную
функции эталонного переходного процесса как 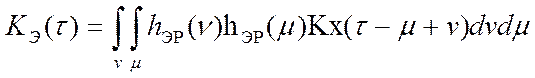 , а автокорреляционную
функции переходного процесса робастной системы как
, а автокорреляционную
функции переходного процесса робастной системы как 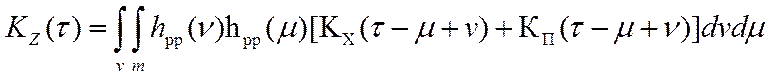 ,
то автокорреляционная функция ошибки цифровой обработки информации в
робастной системе управления запишется как [7, 45]:
,
то автокорреляционная функция ошибки цифровой обработки информации в
робастной системе управления запишется как [7, 45]:
![]()
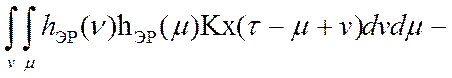
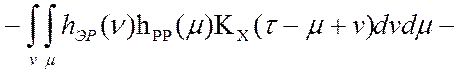
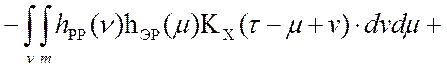
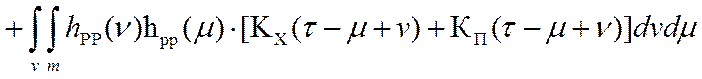 . (4.1)
. (4.1)
Если допустить, что в
качестве эталонного закона регулирования применяется пропорциональный закон, с
динамической характеристикой : ![]() , К1
– настроечный коэффициент эталонного регулятора, то модель (4.1) можно выразить
через динамические характеристики эталонной системы регулирования , hЭР(t), и робастной системы регулирования, hРР(t).
, К1
– настроечный коэффициент эталонного регулятора, то модель (4.1) можно выразить
через динамические характеристики эталонной системы регулирования , hЭР(t), и робастной системы регулирования, hРР(t).
Согласно принятой схеме выделения ошибок цифровой обработки информации (см. рис. 4.1), весовая функция разомкнутой эталонной системы регулирования равна:
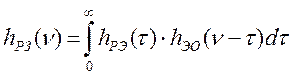 .
(4.2)
.
(4.2)
Амплитудофазовая частотная характеристика (АФЧХ) разомкнутой эталонной системы регулирования примет вид:
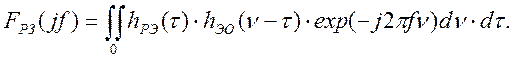 (4.3)
(4.3)
Выражение (4.3) позволяет записать АФЧХ эталонной замкнутой системы управления в виде:
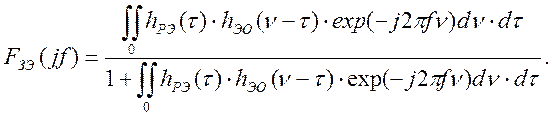
Откуда, весовая функция эталонной замкнутой системы принимает вид:
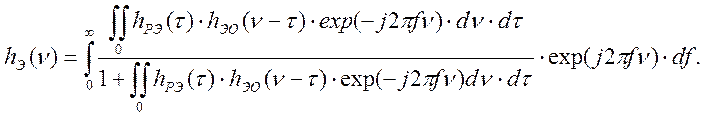 (4.4)
(4.4)
По аналогии с выражением (4.2) весовая функция разомкнутой программно-аппаратной системы регулирования равна:
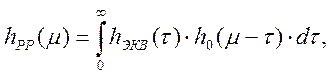
где ![]() -
эквивалентная весовая функция программно-аппаратной системы регулирования.
Весовая функция
-
эквивалентная весовая функция программно-аппаратной системы регулирования.
Весовая функция ![]() может быть вычислена по
соотношению:
может быть вычислена по
соотношению:
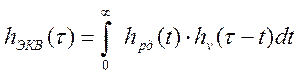 , (4.5)
, (4.5)
где ![]() -
весовая функция цифро-аналогового преобразователя ЦАП (см. рисунок 4.1);
-
весовая функция цифро-аналогового преобразователя ЦАП (см. рисунок 4.1); ![]() - весовая функция программно-аппаратного регулятора,
которая связана с весовой функцией эталонного регулятора как (см. рис.4.1. и [7]):
- весовая функция программно-аппаратного регулятора,
которая связана с весовой функцией эталонного регулятора как (см. рис.4.1. и [7]):
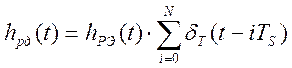 . (4.6)
. (4.6)
Соотношения (4.5) и (4.6) позволяют записать весовую функцию разомкнутой программно-аппаратной системы регулирования в виде [59]:
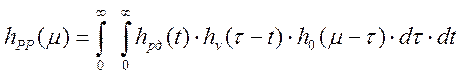 .
.
АФЧХ разомкнутой программно-аппаратной системы, при этом, равна:
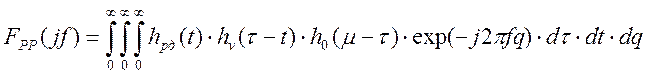 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.