Особенности управления эффективностью функционирования (Глава 1 учебника "Планово-экономическое управление")

                                             Глава 1

        Особенности  управления эффективностью функционирования

Подавляющее большинство технологических процессов содержат аппараты или узлы, обладающие стареющими характеристиками, что приводит  к дрейфу оптимальных режимов функционирования. Вследствие своих внутренних специфических особенностей оптимальный режим технологического процесса случайным образом перемещается в пространстве состояний (дрейфует). Причинами дрейфа являются износ оборудования, старение катализатора, износ инструмента и т.п. Это приводит к неизбежности периодического поиска оптимального режима и свидетельствует о том, что жесткая стабилизация технологических параметров не обеспечивает максимальную  эффективность процессов управления.

                              

 

Рис. 1.1 Структура информационных потоков в робастной системе

( – вектор входных параметров;  – вектор выходных параметров;  – вектор параметров, подлежащих идентификации;  – вектор оптимальных значений управляющего воздействия )

В условиях непрерывного дрейфа характеристик объекта алгоритм  управления должен быть построен так, чтобы на основе измерения текущих входных и выходных параметров процесса постоянно корректировалось значение основных управляющих воздействий (см. рис.1.1). Для любого объекта управления может быть построено и разработано неограниченное количество алгоритмов управления. Качество и эффективность этих алгоритмов зависит, в первую очередь, от уровня знаний об объекте, от полноты априорной информации, сложности объекта, способов получения текущей информации и, конечно же, от интуиции инженера, проектирующего АСУ ТП. Робастные системы управления можно разбить, условно, на три типа, характеризующиеся различным соотношением использования  в них текущей и априорной информации:

1. безмодельные робастные системы; они основаны на обработке данных нормального функционирования объекта, т.е. используют только текущую информацию измеренную на объекте управления;

2. Робастные системы с эталонной моделью используют всю текущую информацию с объекта и часть априорной информации, которая сосредоточена в упрощённой эталонной модели объекта управления;

3. Комбинированные робастные системы  используют всю текущую информацию об объекте и всю априорную информацию в виде полной эталонной модели объекта управления. Основным отличием комбинированной системы является применение безмодельной идентификации положения рабочей точки.

 В безмодельных робастных системах задачи управления решаются по данным нормальной эксплуатации объекта управления. При этом, главным является обеспечение требований наилучшего качества процессов управления в условиях отсутствия эталонного переходного процесса [40].  То есть,  среднеквадратический критерий качества переходного процесса должен быть прогнозируемым:

                                                         

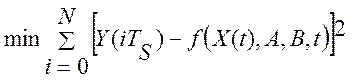
где  Y(iT_S) – наблюдаемый переходный процесс;  – прогнозируемый  (моделируемый) случайный переходный процесс;  Aи B– дрейфующие, в реальном масштабе времени, коэффициенты статической характеристики объекта управления (в линейном случае). Главным, в таких системах, является текущая идентификация положения рабочей точки объекта управления.

Существует большая группа систем, принцип построения которых основан на применении упрощенной эталонной математической модели процесса (аппарата). Текущая информация в таких системах управления используется для идентификации неизвестных параметров эталонной модели, заложенных в математическую модель как физико-химические константы, изменяющиеся в реальном масштабе времени как случайные нестационарные процессы (например, изменения коэффициента теплопередачи в зависимости от толщины накипи на стенках теплообменника). Априорная информация в этих системах формализована в виде упрощённой  математической модели, которая используется дважды сначала для идентификации настроечных коэффициентов математической модели, а затем для отыскания оптимального режима и принятия решения по управлению процессом (см. рис. 1.1). Первый раз эталонная модель используется как процедура идентификации упрощённой модели и решается оптимизационная задача:

                                                     ,                                                            

где   – вектор дрейфующих параметров эталонной модели, подлежащих идентификации;  – функционал невязки между экспериментальными и рассчитанными по упрощённой эталонной модели значениями выходных параметров;  – область допустимых решений (выбирается из априорных знаний об объекте управления). Второй раз эталонная математическая модель используется как процедура поиска оптимального технологического режима:

 

                                                            ,                                                     

где   – оптимальные значения управляющих параметров;  – эталонная математическая модель объекта управления; V- область допустимых значений управляющего воздействия.

В таких системах обязательными является ограничения на время работы процедуры идентификации, , и время работы процедуры оптимизации, . То есть, общее время решения всех задач оптимизации должно быть меньше равно периоду нанесения управляющего воздействия, :