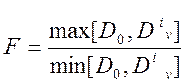Метрологическое обеспечение робастных систем управления (Глава 4 учебника "Планово-экономическое управление"), страница 3

,

где ,  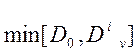– соответственно максимальная и минимальная из дисперсий эталонного и программируемого случайных процессов.

Вычисленное значение F сравнивалось с табличным, F_табл , при данном для каждой дисперсии числе степеней свободы и избранном уровне значимости риска. Число степеней свободы для дисперсии D₀ принималось равно бесконечности, а для  принималось равным длине массива в задаче моделирования. Во всех случаях имитационного моделирования  F < F_табл, следовательно, различие между дисперсиями эталонного и моделируемого случайных процессов можно считать несущественным.

Таким образом, основные метрологические характеристики переходных процесса в робастной системе разбиваются на две группы:

1. Метрологические характеристики информационно-измерительной подсистемы, основное назначение которых - это обеспечение заданной точности измерения всех параметров робастной системы [64];

2. Метрологические характеристики управляющей подсистемы, основное назначение которых является количественная оценка потерь образующихся в процессе управления (см. глава 3);   следует считать, что именно период управления, Т_У, связывает метрологические характеристики модулей УСО в робастной системе в единые количественные оценки качества как алгоритмов текущей идентификации, так и алгоритмов визуализации процессов измерения и управления.

 4.1 Метрологические характеристики измерительной подсистемы

Согласно схеме выделения случайной функции ошибки  цифровой обработки измерительной информации (см. рис. 4.5 и [7, 58, 64])  фактический эффект воздействия информационного дискретно-непрерывного канала на исходный непрерывный случайный  процесс естественно рассматривать по отношению к результату применения желаемой непрерывной линейной операции (передачи, фильтрации) к исходному непрерывному сигналу. Реализация соответствующей случайной функции ошибки (рис. 4.5) может быть представлена в виде:

,                                     

где   и  – частные реализации выходного сигнала реального дискретно-непрерывного и эталонного каналов. Для наиболее часто встречаемых, в технических системах, допущений о нормальности и стационарности  (по  крайней  мере,  в  широком  смысле)  исходного измеряемого сигнала, в силу линейности его преобразований в функции  и , случайная функция ошибки  также является нормальной и стационарной. Стационарность случайной функции ошибки  по математическому ожиданию следует непосредственно из стационарности по математическому ожиданию исходного процесса 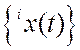 [7, 20, 34]: .  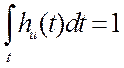Предполагая весовую функцию эталонного канала  нормированной:   и используя равенство , получаем:

 

   .

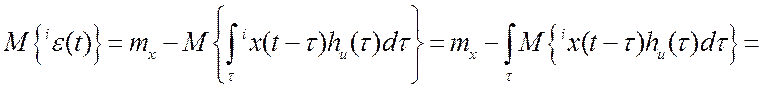
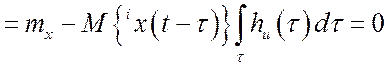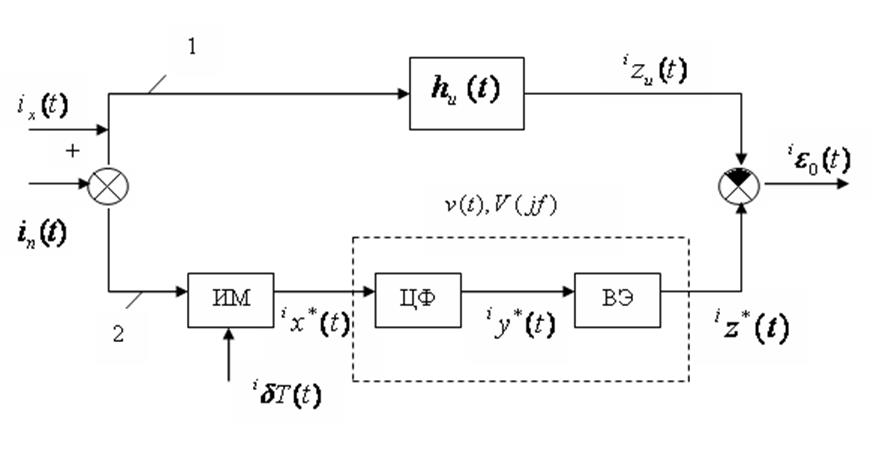
Рис. 4.5 Схема выделения случайной функции ошибки  (ИМ – импульсный модулятор, ЦФ – программный фильтр; ВЭ – восстанавливающий элемент).

Если все вероятностные свойства случайной функции  определены,  то известна корреляционная функция ошибки  [Ш]:

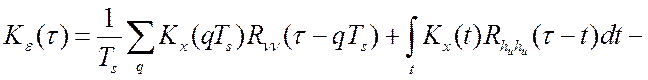
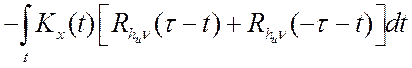               .                                           (4.13)

Отсюда, в частности, с учетом соотношения 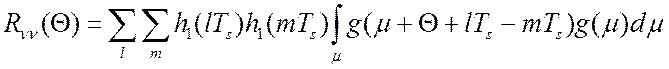 для дисперсии ошибки имеем [64]:

                    

      

      

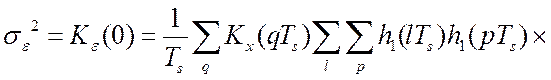
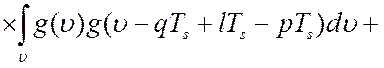
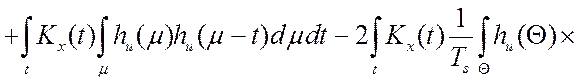
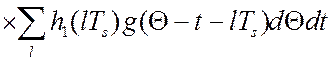       .                                                  (4.14)                                                                                              

Корреляционную функцию ошибки К_ε(τ) можно представить также через соответствующие характеристики в частотной области [58]:

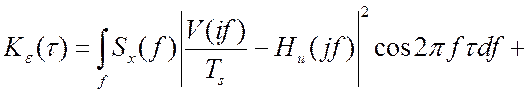
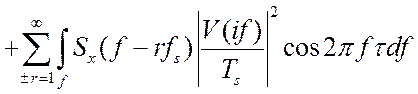         .                                  (4.15)

Отсюда дисперсия ошибки определяется выражением:

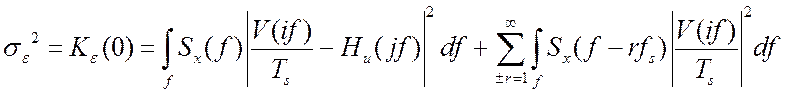  .   (4.16)