Метрологическое обеспечение робастных систем управления (Глава 4 учебника "Планово-экономическое управление"), страница 4

Модели 4.13 -:- 4.16  в явной форме характеризуют структуру и механизм появления флуктуационной динамической ошибки при дискретной передаче и обработке непрерывных несингулярных сигналов. Эти выражения, как нетрудно видеть, позволяют получить количественное описание точности дискретно-непрерывного канала для любых желаемого и реализующих его дискретно-непрерывных операторов, задаваемых своими временными или частотными характеристиками.

 Переходя к последовательности показаний эталонного информационно-измерительного канала, Y(t), и последовательности показаний программно-аппаратного измерительного канала, Z(t) , информационно-измерительной подсистемы АСУТП дисперсию ошибки цифровой обработки измерительной информации можно записать как:

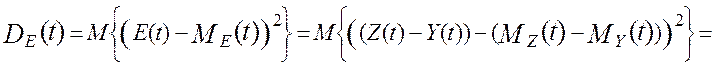
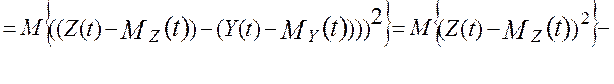
                                   ,                       (4.17)

Таким образом, методическая динамическая составляющая  погрешности цифровой обработки измерительной информации в информационно-измерительном канале полностью определяется тремя основными метрологическими характеристиками информационно-измерительной подсистемы АСУТП -  это  дисперсией показаний программно-аппаратного измерительного канала, D_Z(t), дисперсией показаний эталонного информационно-измерительного канала, D_Y(t), и взаимокорреляционной функцией этих показаний , K_ZY(t,t).

          На рисунке 4.6. представлена типовая структура программно-аппаратного измерительного канала робастной системы. Допустим, что  - текущее значение автокорреляционной функции измеряемой величины ,  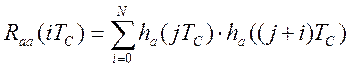 - корреляционная функция динамической характеристики аналоговой части программно-аппаратного канала, 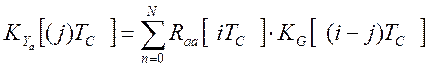 - автокорреляционная функция  аналоговой части и измерительного канала,   а 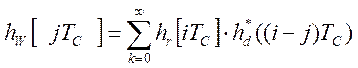 -   взаимокорреляционная функция решетчатых весовой функции  восстанавливающего элемента и весовой функции программного динамического оператора. Тогда, автокорреляционная функция показаний программно-аппаратного измерительного канала будет иметь вид [56]:

,

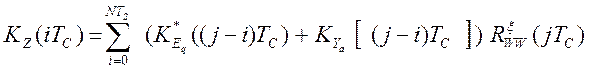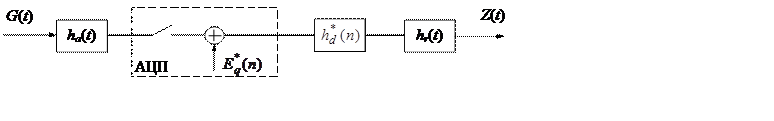
Рис. 4.6 Структура программно аппаратного измерительного канала

Учитывая, что корреляционная функция ошибки квантования по уровню отлична от нуля только при значении аргумента равном нулю [7]:

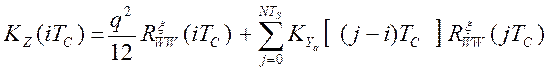        ,                            (4.18)

 где 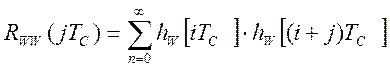 - это корреляционная функция непрерывной весовой функции , которая относится к классу решетчатых функций  и является эквивалентной весовой функцией цифровой части программно-аппаратного измерительного канала и восстанавливающего элемента. Первое слагаемое в выражении (4.18) обусловлено наличием ошибки квантования по уровню в аналого-цифровом преобразователе, второе слагаемое отражает стохастические свойства входного воздействия G(t).

       Таким образом, в общем случае реакция программно-аппаратного измерительного канала 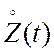 на стационарное входное воздействие 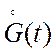 является  нестационарным случайным процессом. Однако стационарной является случайная последовательность, представляющая собой совокупность значений центрированного выходного сигнала 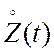 измерительного канала в моменты времени t = iT_S, при фиксированном значении  T_C ,      где 0 £ T_C < 1 ( 0.33 сек, 0.66 сек, 1 сек) [7].  Следовательно, стационарной будет  и случайная последовательность, которая  представляет  собой значения функции 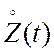 в моменты времени:   , где  x -это случайное число в диапазоне 0 £ x < 1, а  i – целое число (порядковый номер элемента в массиве). Корреляционную функцию последовательности 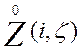 будем обозначать , подчеркивая тем самым, что она существует только при значениях аргумента, кратных T_s, и при этом значения функции зависят от параметра x, который можно трактовать номер реализации при усреднении по множеству реализаций или как случайную фазу при усреднении по одной реализации.    Таким образом, автокорреляционная функция показаний программно-аппаратного канала зависит от обоих своих аргументов t и t, а это означает, что случайная функция 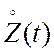 является нестационарной.