Метрологическое обеспечение робастных систем управления (Глава 4 учебника "Планово-экономическое управление"), страница 2

Отсюда АФЧХ  замкнутой программно-аппаратной системы регулирования  может быть выражена как:

 .             

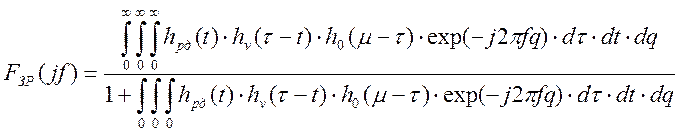Тогда весовая функция замкнутой программно-аппаратной системы регулирования примет вид [27]:

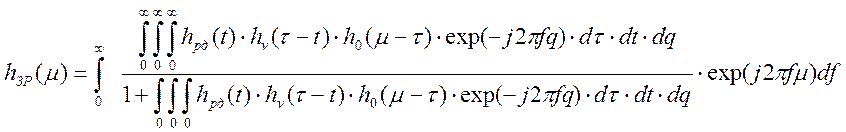 (4.7)

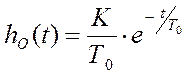Учитывая допущения о том, что , весовая функция объекта управления описывается выражением: , весовая функция разомкнутой эталонной системы регулирования будет равна:

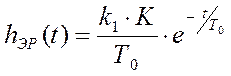,                                           (4.8)

где k₁  – настроечный коэффициент пропорционального закона управления, K – коэффициент передачи объекта управления, Т₀  -постоянная времени объекта по каналу управления.

Передаточная функция разомкнутой эталонной системы регулирования равна:

               ,                                        

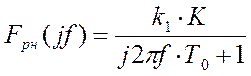а передаточная функция замкнутой эталонной системы регулирования:

 .                                  

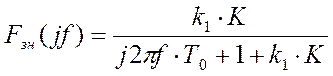Результат обратного преобразования Фурье от выражения  дает:

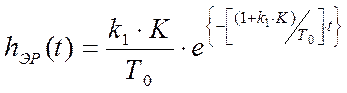.                                      (4.9)

Если принять [59], что АЦП (см. рис. 4.1) реализует процесс измерения управляющего воздействия с помощью прямоугольного импульса: 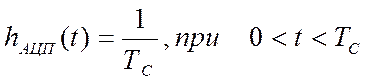, то, на основании модели образования цифровой последовательности (4.6) и рассмотрении одного интервала Т_S, 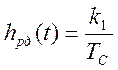. Здесь T_C – это настроечный коэффициент АЦП (время одного измерения).

Отсюда следует, что весовая функция разомкнутой программно- аппаратной системы регулирования принимает вид:

.                    

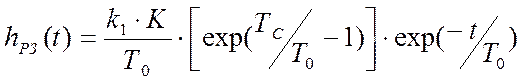Преобразование Фурье от этой весовой функции и получение передаточной функции замкнутой программно-аппаратной системы регулирования дает следующий результат:

.                                       

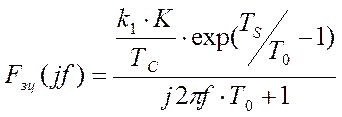Результат обратного преобразования Фурье от данного выражения есть искомая весовая функция замкнутой программно-аппаратной системы регулирования:

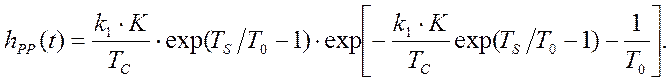              (4.10)

Подстановка (4.9) и (4.10) в математическую модель (4.1) приводит нас к математической модели образования ошибок цифровой обработки измерительной информации в робастной системе регулирования:

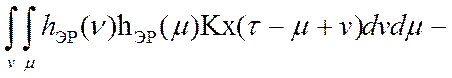
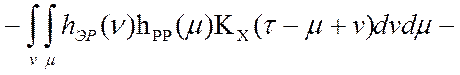
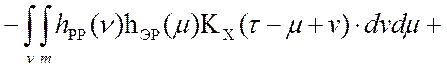
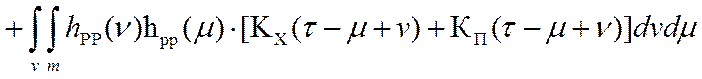 .          (4.11)

Если обозначить за =1/Т₀   скорость изменения сигналов в объекте управления и ввести типовые константы :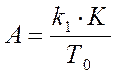 , , 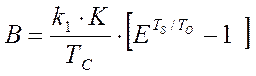 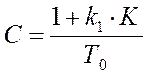и 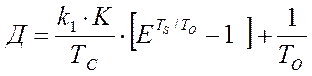, то относительная погрешность робастной стабилизации, в смысле методической динамической ошибки цифровой обработки измерительной информации в робастной системе примет вид [27, 59]:

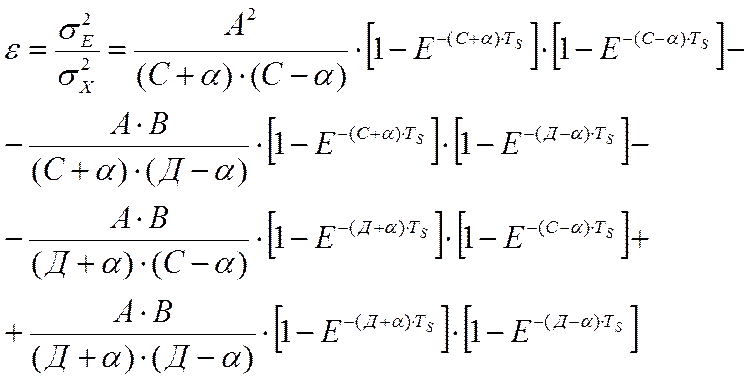      (4.12)

На рисунке 4.2 (сплошная линия) представлен график зависимость ошибки цифровой обработки измерительной информации, полученный расчетом по математической модели (4.12) от относительного темпа обработки информации в робастной системе, αT_S  [27]. Достоверность полученных результатов в работе проверялась методом имитационного моделирования, согласно методике из работы [23]. На рисунке 4.4 результаты имитационного моделирования представлены крестиками. Анализ результатов моделирования показывает, что в области малых значений αTs наблюдается плато с погрешностью отработки информации на уровне сотых долей процента. Это говорит о том, что именно в том диапазоне аргумента лежат оптимальные значения времени измерения, T_C , всех переменных задействованных в критерии управления. Увеличение периода опроса датчиков, T_S , приводит к снижению погрешностей обработки информации. Это сказываются фильтрующие свойства объекта управления, обратных связей, а, главное фильтрующей способности операции дискретизации.

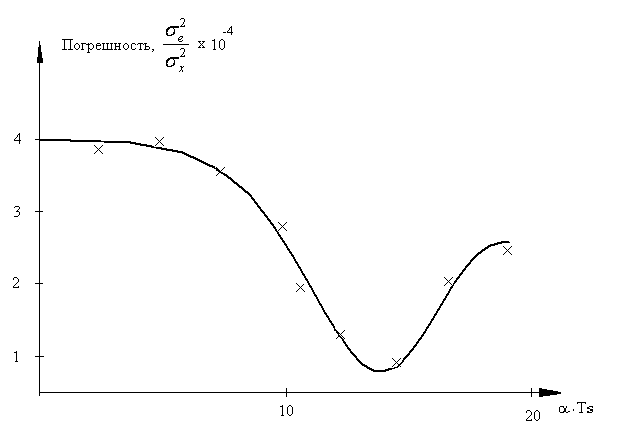
Рис. 4.4  Ошибки цифровой обработки измерительной информации

Поэтому при проектировании робастных систем управления  период нанесения управляющих воздействий, Т_У,  должен выбираться с учетом динамических свойств объекта управления:  (T_O – постоянная времени динамической характеристики объекта управления). Проверка достоверности полученных результатов проводилась с помощью F- критерия Фишера [27]. В частности, осуществлялась проверка равенства дисперсии, D_vⁱ,  i-того моделируемого экспериментального случайного процесса V(t), с величиной D₀  эталонного экспериментального случайного процесса. С этой целью вычислялось отношение