1.3 Особенности метрологического обеспечения робастных систем
С точки зрения надёжности функционирования робастные системы проектируются как распределённые. Степень сосредоточенности, при этом зависит только от сложности критерия управления технологическим процессом и сложности критериев оценки эффективности отдельных аппаратов и узлов. При этом, метрологические характеристики полностью определяются теоремами Ляпунова А.М. о возмущенном и невозмущенном движениях.
|
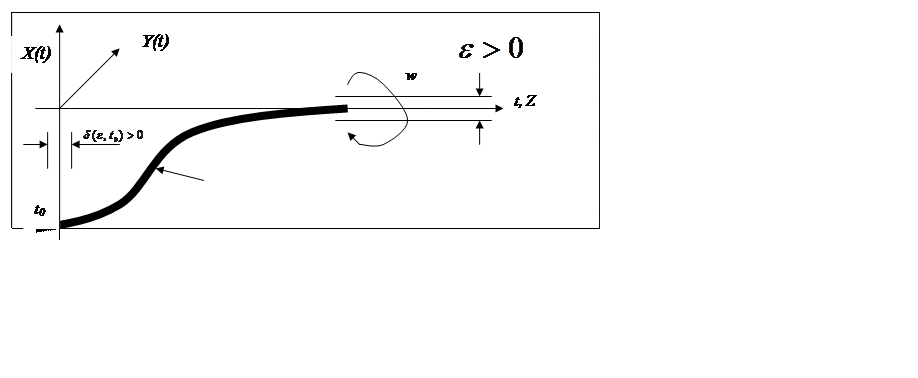
Рис. 1.10 Геометрическая интерпретация робастной устойчивости.
На
рисунке 1.10 представлена модельная траектория движения объекта управления с
пятимерной эталонной математической моделью. Пусть известно решение системы F (X,Y,Z,t,w) (на рисунке
1.10 жирная линия). Это решение будем называть программным (эталонным). Любое
отличие от этого эталонного движения будем называть возмущённым движением.
Тогда, согласно Ляпунову А.М. невозмущенное движение F0(t) называется
устойчивым, если для любого ![]() и любого числа
и любого числа ![]() можно
указать число
можно
указать число ![]() , такое, что при норме разности
, такое, что при норме разности ![]() будет выполняться неравенство
будет выполняться неравенство ![]() при
при ![]() , где
, где ![]() -это возмущенное движение, проходящее
через точку
-это возмущенное движение, проходящее
через точку ![]() в момент реального времени
в момент реального времени ![]() . Здесь под нормой понимается
. Здесь под нормой понимается 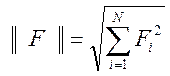 . При этом, если коэффициенты эталонной
модели дрейфуют случайным образом, то согласно второму началу Ляпунова, невозмущенное движение F0(t) называется
асимптотически устойчивым, а величину ∆0
для любого ∆ >0 можно выбрать так, что (см. рис. 1.11):
. При этом, если коэффициенты эталонной
модели дрейфуют случайным образом, то согласно второму началу Ляпунова, невозмущенное движение F0(t) называется
асимптотически устойчивым, а величину ∆0
для любого ∆ >0 можно выбрать так, что (см. рис. 1.11):
![]() .
.
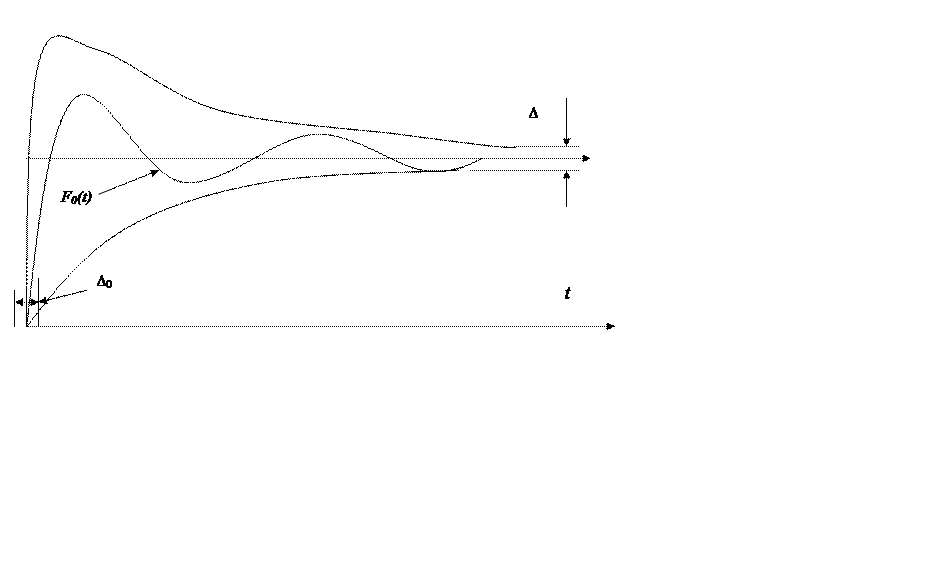
Рис. 1.11. К понятию случайной фазы возмущенного движения
Величину ∆0 будем называть случайной фазой начала движения [7]. Это позволяет применить теорию потенциальной помехоустойчивости Котельникова А.В. [18] для описания метрологических характеристик переходных процессов в робастной системе адаптивного управления (см. глава 4).
Расчету динамических погрешностей в таких интеллектуальных измерительных и управляющих системах уделяется много внимания. В работах [12, 17, 41, 42, 43] для исследования погрешностей обработки информации в информационно-измерительных подсистемах АСУТП применяется схема выделения ошибок дискретного представления информации в системе управления, согласно которой за ошибку обработки информации принимается разность между оцифрованным случайным процессом и аналоговым случайным процессом как эталоном сравнения. Тогда за математическую модель формирования динамических погрешностей в измерительном канале можно принять выражение для корреляционной функции ошибок обработки информации реальным техническим каналом по отношению к эталонному (идеальному) каналу обработки информации. Корреляционную функцию ошибки обработки информации реальным техническим каналом по отношению к эталонному (идеальному) каналу обработки информации можно принять в качестве критерия работоспособности интеллектуальных измерительных и управляющих систем [45] при имитационном моделировании.
Фактический эффект
воздействия непрерывно-дискретно-непрерывного информационно-измерительного
канала на исходный непрерывный случайный процесс измерения любой физической
величины естественно рассматривать по отношению к результату применения
эталонной непрерывной линейной динамической операции передачи к исходному
непрерывному сигналу. Реализация соответствующей случайной функции ошибки может
быть представлена в виде разности [35]: ![]() , где
, где ![]() и
и ![]() – частные
реализации эталонной и программно-аппаратной системы измерения критерия
управления (виртуального прибора).
– частные
реализации эталонной и программно-аппаратной системы измерения критерия
управления (виртуального прибора).
Стационарность случайной
функции ошибки, ![]() , по математическому ожиданию
следует непосредственно из модели выделения ошибки:
, по математическому ожиданию
следует непосредственно из модели выделения ошибки: ![]() . Откуда следует, что математическое
ожидание функции ошибки равно:
. Откуда следует, что математическое
ожидание функции ошибки равно: ![]() .
.
В работах [7, 45, 58] было показано, что ошибки цифровой обработки информации при типовых моделях элементов программно-аппаратного измерительного канала (см. глава 2.2) имеют автокорреляционную функцию:
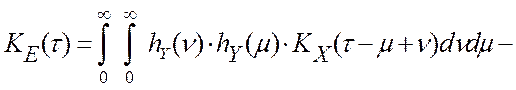
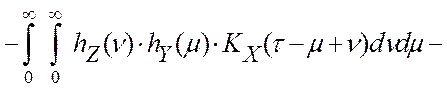
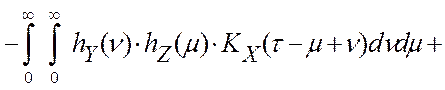
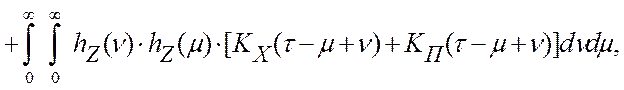
где KX (t) и KП (t) – соответственно автокорреляционные функции управляющего
воздействия и помехи измерения, обладающие свойствами четности, т.е. ![]() , а
, а ![]() . При
этом, даже при допущении о стационарности случайного измерительного сигнала все
метрологические характеристики измерительного канала являются нестационарными
функциями, а модель автокорреляционной функции ошибки, при τ=0, принимает
следующий вид [61]:
. При
этом, даже при допущении о стационарности случайного измерительного сигнала все
метрологические характеристики измерительного канала являются нестационарными
функциями, а модель автокорреляционной функции ошибки, при τ=0, принимает
следующий вид [61]: ![]()
![]() , из которого следует, что методическая
динамическая составляющая погрешности цифровой обработки измерительной информации
в информационно-измерительной подсистеме АСУТП полностью определяется тремя
основными метрологическими характеристиками измерительной системы – это дисперсия
показаний информационно - измерительной подсистемы АСУТП, DZ(t), дисперсия показаний эталонной
информационно-измерительной системы, DY(t) и взаимокорреляционной функцией этих показаний
, KZY(t,t).
, из которого следует, что методическая
динамическая составляющая погрешности цифровой обработки измерительной информации
в информационно-измерительной подсистеме АСУТП полностью определяется тремя
основными метрологическими характеристиками измерительной системы – это дисперсия
показаний информационно - измерительной подсистемы АСУТП, DZ(t), дисперсия показаний эталонной
информационно-измерительной системы, DY(t) и взаимокорреляционной функцией этих показаний
, KZY(t,t).
Невозможно создать робастную
систему управления без применения критерия управления, привязанного к
параметрам функционирования измерительных каналов. Эти критерии, как правило,
представляют собой обобщенные критерии качества управления. Так, например [19],
при создании виртуального прибора по измерению количества потреблённого тепла ![]() в уравнение измерения входят четыре измерительных
канала и восемь параметров определяющих режимы работы системы в целом (периоды
опросов датчиков и постоянные времени фильтров):
в уравнение измерения входят четыре измерительных
канала и восемь параметров определяющих режимы работы системы в целом (периоды
опросов датчиков и постоянные времени фильтров):
![]() ,
,
где G1 (t)– расход теплоносителя в подающем трубопроводе; G2 (t)– расход теплоносителя в обратном трубопроводе, возвращенного производителю; Т1(t) и Т2 (t)– температуры воды в подающем и обратном трубопроводах; ср – средняя изобарная теплоемкость воды.
При управлении котлоагрегатами на тепловых электрических станциях важно иметь вторичный прибор по измерению текущих значений эффективности работы котлоагрегата, который функционирует по уравнению измерения [11]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.