,
где 
(t) – текущее значение количества
выработанного тепла, 
(t) – текущее значение количества тепла, прогнозируемого по
математической модели котлоагрегата.
В работе [27] критерием
управления процесса получения эндогаза выбран технологический коэффициент
полезного действия эндогазогенератора (текущая эффективность), ЭР(t), который предлагается оценивать по отношению текущего
значения влажности эндогаза, измеряемого влагомером, 
,
к текущему значению влажности, рассчитанному по математической модели
эндогазогенератора, 
:
.
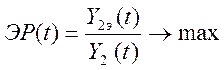Анализ схемы движения информационных потоков в эндогазогенераторе и динамических свойств эндогазогенератора по основным каналам управления и измерения показал, что текущее значение эффективности работы газогенератора определяется следующим уравнением измерения [27]:
,
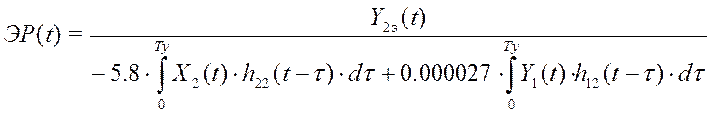где Y2э (t)–значение влажности, измеренное влагомером, X2(t) – текущие значения расхода воздуха в газовоздушной смеси; Y2(t) – текущие значения влажности эндогаза измеренные промышленным прибором; Y1(t) – текущие значения температуры в реторте генератора; h22(t) – импульсная переходная характеристика по каналу управления влажностью эндогаза; h12(t) – импульсная переходная характеристика по каналу влияния температуры реторты на влажность, Tу – период идентификации динамических характеристик эндогазогенератора, который тесно связан с темпом обработки измерительной информации в информационной подсистеме АСУТП.
Если анализировать информативность и эффективность интеллектуальной измерительной техники [65] виртуальных приборов, то она прямо пропорционально сложности критерия управления. При этом, размерность решаемой задачи моделирования равна числу измерительных каналов виртуального прибора.
Достоверность же показаний виртуального прибора обеспечивается в процессе его проектирования. При этом целесообразно использовать типовую структуру измерительного канала, обеспечивая тем самым, высокую информативность и надежность функционирования виртуального прибора. С целью снижения рисков получения не адекватных результатов измерения математические модели объектов, элементов измерительных каналов, включая модели сигналов и измеряемой среды, должны выбираться как можно проще, чтобы скорость обработки информации по разным каналам была соизмерима со скоростью генерации этой информации в объекте управления. Особые требования предъявляются, при этом, к математической модели формирования динамической погрешности в измерительной системе, так как она в дальнейшем используется как критерий оптимизации режимных параметров работы всей управляющей системы.
В работах [24, 58] получена модель методической динамической погрешности измерения виртуального прибора с M измерительными каналами и длинной массива, N. Модель раскрыта через настроечные коэффициенты виртуального прибора при допущениях о стационарности измеряемых сигналов и безинерционной передачи информации в эталонной измерительной системе:
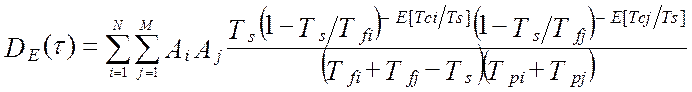
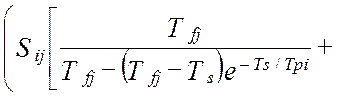
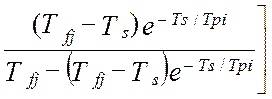
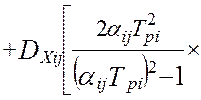
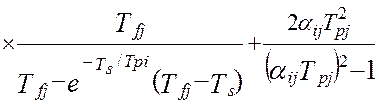
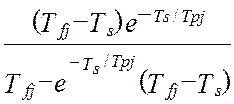
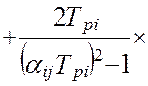
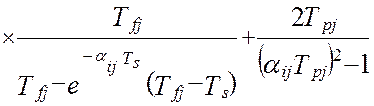
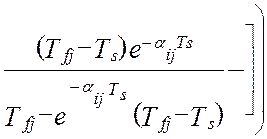
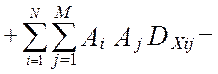
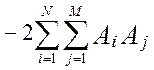
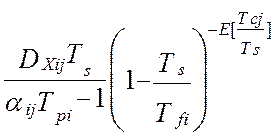
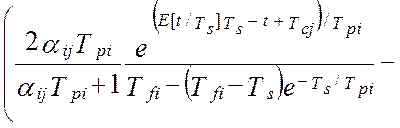
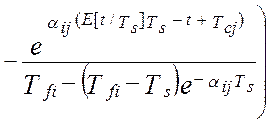
В этой модели : Ai ,Aj – настроечные коэффициенты измерительной системы (являются функциями коэффициентов линеаризации уравнения измерения и коэффициентов статических характеристик датчиков информации); TS – единый период опроса датчиков; Tfi– постоянные времени программных динамических преобразователей; Tpi– постоянные времени динамических характеристик датчиков; αij– квадратная матрица скоростей изменения измеряемых величин; E[t/TS] – дискретное время (операция взятия целой части числа); Sij– матрица помех измерения; DXij– корреляционная матрица измеряемых сигналов при t=0, в которой диагональные элементы –это дисперсии измеряемых сигналов, все остальные элементы матрицы - это коэффициенты корреляции показаний датчиков.
В работе [27] эта модель была подтверждена на адекватность методом имитационного моделирования. На рисунке 1.12 представлена зависимость ошибки цифровой обработки одного измерения в массиве показаний виртуального прибора для измерения критерия управления. Казалось бы, что ошибка мала (минимум равен 0.005%). Однако следует помнить, что для идентификации динамических характеристик объектов управления, уже при длине массива в 100 измерений ошибка будет около 0,5%. А это уже соизмеримо с погрешностями измерения.
Поэтому при создании робастных систем существует другая группа метрологических характеристик, которые характеризуют ошибки, возникающие в процессе проектирования системы управления. К ним относится ошибки идентификации (см. рис.1.12), которые определяются настроечными коэффициентами измерительных каналов и в первую очередь темпом обработки информации, TS . Большое значение имеет учёт ошибок, возникающих при линеаризации критерия управления (см. рис. 1.13). Этот вид методической ошибки зависит от положения математического ожидания управляющего воздействия в пространстве состояния объекта управления.
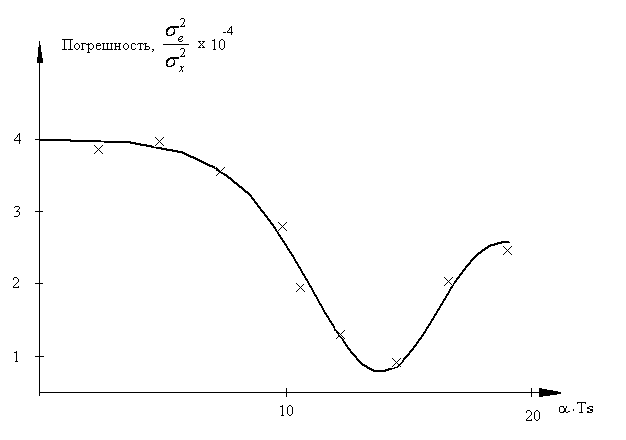
Рис. 1.12 Ошибки цифровой обработки измерительной информации [27]
 |
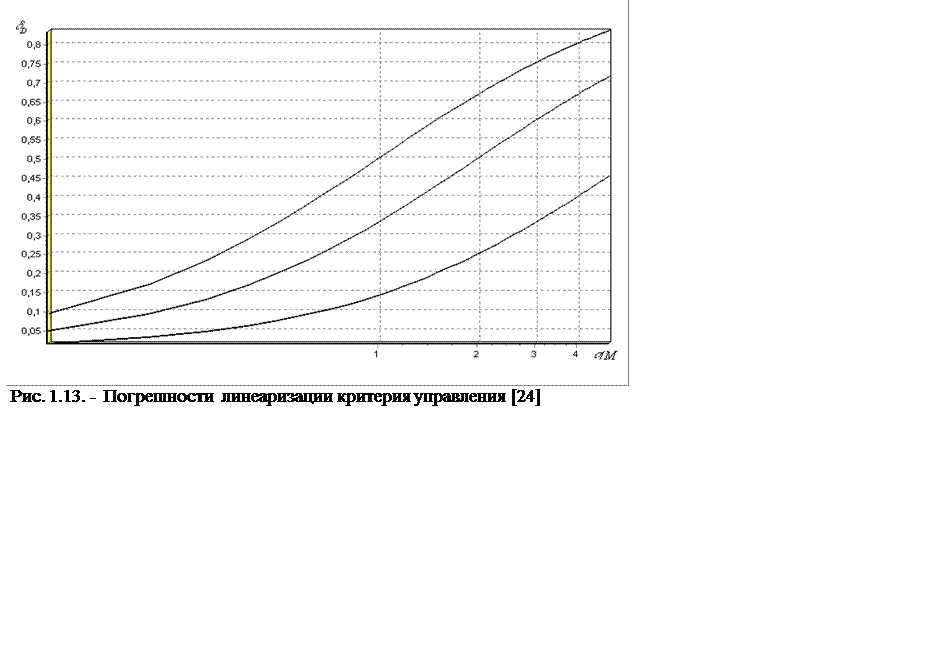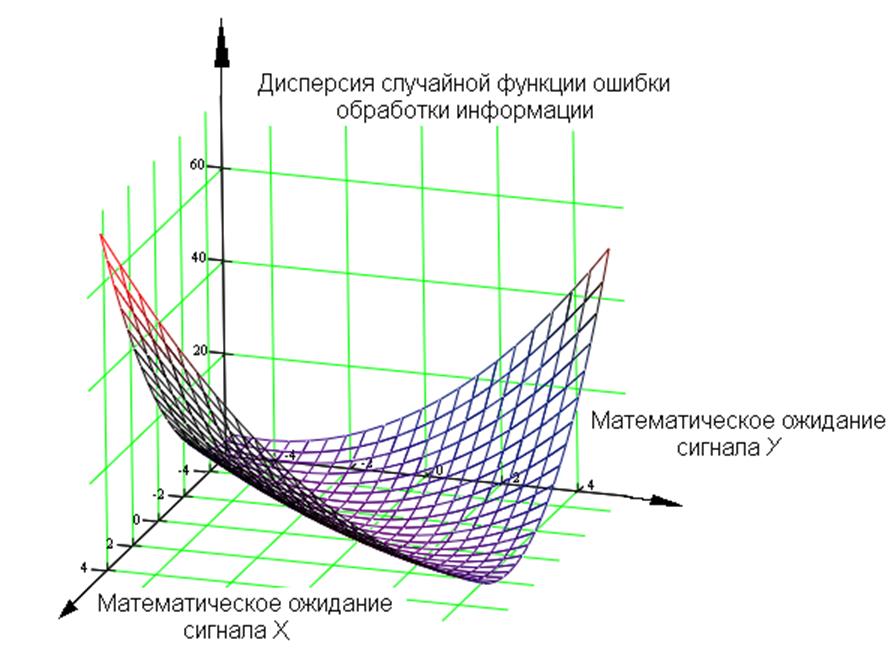
Рис. 1.14– Ошибки текущей идентификации [27]
И на конец, ошибки имитационного моделирования (см. рис.1.14), которые определяются в основном квалификацией проектировщиков робастной системы. Таким образом, при анализе результатов проектирования робастных систем необходимо просматривать все три типа моделируемых переходных процесса (см. рис.1.15). Конечно же, главный – это эталонный переходный процесс (см. жирную линию-1 на рисунке 1.15), как цель которую необходимо достигнуть в процессе управления. Линия 3 на рисунке 1.15 – это переходный процесс, полученный в результате имитационного моделирования процессов управления по заданному(спроектированному) алгоритму управления. Пунктиром 2 на рисунке 1.15 показан переходный процесс, полученный в результате имитационного моделирования процесса управления при оптимальных настройках всех алгоритмов системы.
|
|
Рис. 1.15 Прогнозируемые переходные процессы адаптивного управления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
