Методические ошибки моделирования процессов управления (Раздел 4.3.2 учебника "Планово-экономическое управление")

4.3.2 Методические ошибки моделирования процессов управления

           Замена физических экспериментов по исследованию метрологических характеристик программно-аппаратных измерительных приборов и систем, имитационным моделированием ставит проблему создания специальных стендов для имитации процессов управления [29]. Ядром такого стенда является пакет прикладных программ, который должен обеспечить  моделирование динамических свойств объекта управления, имитацию свойств измерительной информации как случайных процессов в реальном масштабе времени. Кроме того, в базе знаний такого пакета прикладных программ должны  хранятся модели элементов программно-аппаратного измерительного канала, модели эталонных измерительных каналов и модели критериев управления.  Блок управления имитационным моделированием такого пакета предназначен для планирования и контроля процесса измерения и моделирования. В его функции входит задание параметров для остальных блоков пакета прикладных программ, визуализация результатов моделирования и измерения, организация диалога с оператором, организация, при необходимости, цикличности процесса моделирования с изменением параметров моделирующих алгоритмов. Таким образом, основные погрешности представления непрерывных функции их решётчатым аналогом связаны с дискретизацией измерительной информации. Например, погрешность воспроизведения корреляционной функции при моделировании можно определить как разность оценки моделируемой корреляционной функции и истинной корреляционной функции:

где   - оценка корреляционной функции по усеченной реализации; - погрешность от квантования по уровню; - погрешность от не идеальности датчика независимых случайных величин.

           Если определить методическую динамическую погрешность метода моделирования случайного процесса как: , то методическая динамическая погрешность моделирования случайного процесса будет равна:

Рассмотрим свойства методической погрешности моделирования эргодических стационарных процессов, у которых предел оценки корреляционной  функции стремится к истинной корреляционной функции при бесконечно большой длине реализации

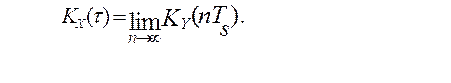
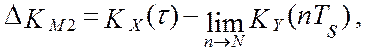Это дает основание выделить две составляющие методической погрешности моделирования - это погрешность DK_M1 за счет усечения корреляционной функции и погрешность DK_M2 за счет процесса измерения, которая определяется свойствами измерительного прибора: , где:   а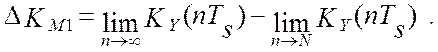 

Анализ этих составляющих погрешности показывает, что погрешность от квантования по уровню,, в силу допущений принятых к модели АЦП [58], равна нулю. Близка к нулю и погрешность,  формируемая генератором независимых случайных величин,  . Следовательно, все погрешности имитационного моделирования формируются методом моделирования случайного процесса, а методическая динамическая погрешность моделирования измерительной информации зависит только от длины моделируемой реализации и  периода опроса датчика, T_s. Таким образом, для моделирования измерительной информации необходимо и достаточно задаваться длиной реализации, N, периодом опроса датчиков, T_s и  относительной методической погрешностью имитационного моделирования: 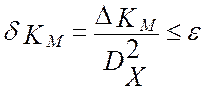. Итак, основная погрешность имитационного моделирования, как процесса измерения, так и процессов управления, возникает при программно-аппаратной реализации аналогового эталонного канала измерения и приближенной замене аналогового измерительного преобразователя его программной реализацией (см. рис. 4.11). В результате этих замен  вычисление значений сигнала Y(t) на выходе эталонного измерительного канала производятся в точках t=it₀и полностью определяются периодом дискретизации t₀ (быстродействие выбранной ЭВМ, которое является аналогом времени измерения в АЦП программно-аппаратного измерительного канала, T_c). Таким образом, показаниями эталонного моделируемого измерительного канала являются элементы дискретной последовательности , Y^*(nt_o) , которые отличаются от вычисленных значений последовательности показаний программно-аппаратного измерительного канала, Z^*(n), на величину ошибки E^*(n)=Y^*(nt₀)-Z^*(n). Эта последовательность ошибок  обусловлена, в первую очередь, темпом обработки информации в моделируемом программно-аппаратном измерительном канале, T_s. В пределе, при t₀®0 процессы в аналоговом преобразователе и его программной реализации совпадают, поэтому период генерации очередного значения измерительной информации должен совпадать с временем измерения, T_c удовлетворяющему заданной точности моделирования или быть кратным ему [64].

          На рисунке 4.11 показана схема формирования погрешности имитационного моделирования аналогового измерительного преобразователя, на вход которого воздействует стационарный случайный процесс, X(t).           Пусть линейный аналоговый измерительный преобразователь с весовой функцией h(t), на вход которого воздействует стационарный случайный процесс X(t), моделируется программным преобразователем в виде последовательности весовых коэффициентов h(n). Ошибка моделирования, которую можно рассматривать как выходной сигнал измерительной системы, представленной на рис. 1, будет равна: E^*(n)=Y(nt₀)-Z^*(n), где Y(nt₀) – последовательность показаний эталонного измерительного прибора, Z^*(n) –  последовательность показаний программно-аппаратного измерительного прибора.