Методические ошибки моделирования процессов управления (Раздел 4.3.2 учебника "Планово-экономическое управление"), страница 2

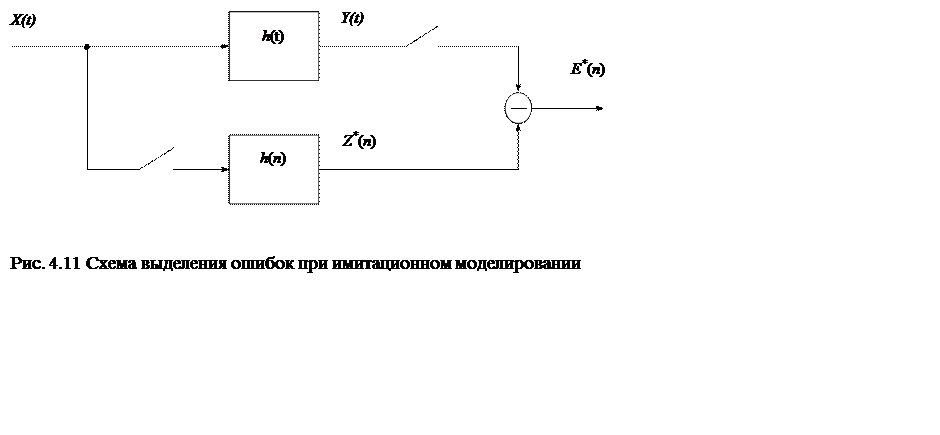
Учитывая, что показания эталонного прибора определяется как 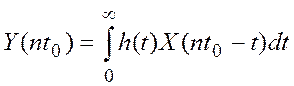, а показания программно-аппаратного прибора как

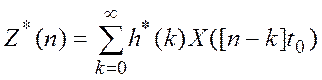, последовательность ошибок моделирования процесса измерения будет равна:

                       .

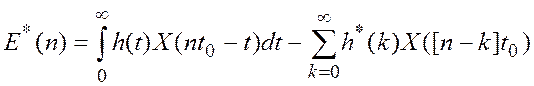Отсюда дисперсия ошибки моделирования процесса измерения  равна [12]:

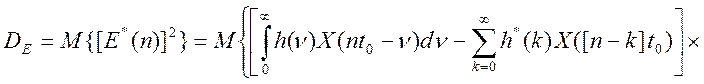
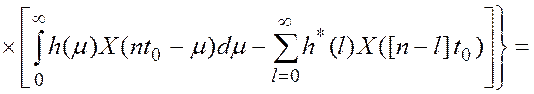
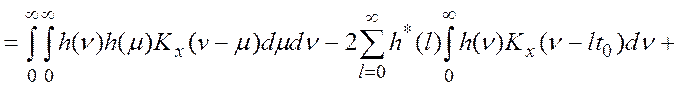
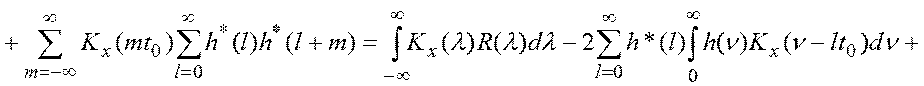
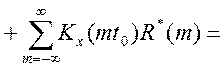
                                                  (4.36)

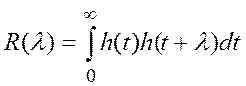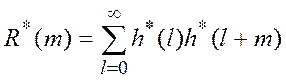где: K_X(t) –  это автокорреляционная функция случайного процесса X(t);    - это автокорреляционная функция весовой функции эталонного прибора;  - автокорреляционная функция последовательности весовых коэффициентов программного динамического преобразователя;  D_Y – дисперсия показаний эталонного прибора; K_YZ(0) – взаимокорреляционная функция последовательности показаний эталонного прибора и последовательности показаний программно-аппаратного прибора;  D_Z- дисперсия последовательности показаний виртуального прибора .

          Относительная среднеквадратическая погрешность моделирования процесса измерения  эталонным прибором будет равна .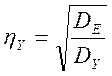

     Пусть динамическая характеристика эталонного прибора обладает весовой 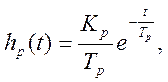функцией:   а на вход этого прибора воздействует измерительная информация в виде стационарного случайного процесса X(t) с экспоненциальной корреляционной функцией: .  Массив весовых коэффициентов программного динамического преобразователя может быть получен, методом дискретного преобразования Лапласа  весовой функции эталонного прибора (см. глава 2), а соответствующая последовательность весовых коэффициентов: .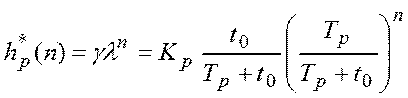        

Тогда дисперсия последовательности показаний  программно-аппаратного прибора Z^*(n) будет равна [12]:

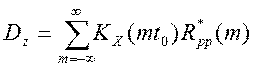
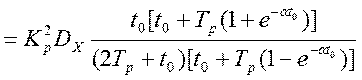                    .           (4.37)

          Дисперсия показаний эталонного прибора Y(t) равна значению автокорреляционной функции показаний эталонного прибора в нуле [12]:

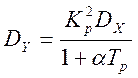                                               .                                               (4.38)

Взаимокорреляционная функция показаний эталонного прибора Y(t) и последовательности показаний программно-аппаратного прибора, Z^*(n), при нулевом значении аргумента равна [12]:

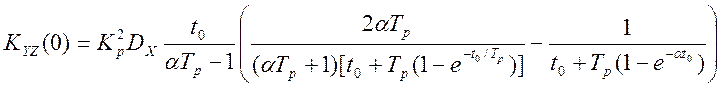        .          (4.39)

          Подстановка (4.37), (4.38) и (4.39) в (4.36), дает выражение для количественной оценки  дисперсии ошибки имитационного моделирования аналогового (эталонного) динамического преобразователя  с помощью программного динамического преобразователя:

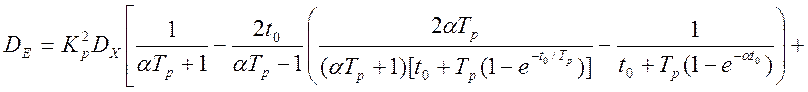
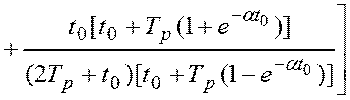.                                                                      (4.40)

          Как видно, из этой метрологической характеристики (4.40) погрешность моделирования процессов измерения и свойств эталонного аналогового прибора зависит не только от настроек эталонного прибора K_p , T_p и свойств измерительной информации,  D_X  и a. Она зависит, так же и от настроек программно-аппаратного канала, то есть шага дискретизации моделируемого случайного процесса, t₀, длины массива весовых коэффициентов программного динамического преобразователя, N, и количества моделируемых реализаций, k.

          В силу допущений об аддитивном воздействии помехи на результат измерения полезного сигнала дисперсия ошибки моделирования процесса измерения будет равна: D_E=D_EX +D_EП, где  - дисперсия ошибки моделирования эталонного прибора, на вход которого воздействует только полезный сигнал X(t);  - дисперсия ошибки моделирования эталонного прибора , на вход которого воздействует только помеха  П(t).

Для случая, когда автокорреляционные функции полезного сигнала и помехи имеют экспоненциальный вид: , , дисперсия ошибки имитационного моделирования процесса измерения  будет равна [12]:

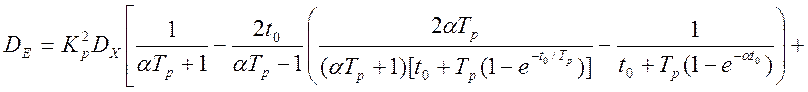
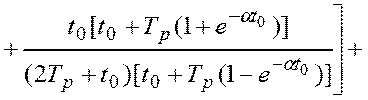
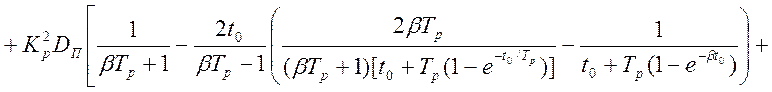
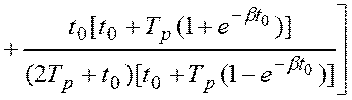.                                                                    (4.41)