Методические ошибки моделирования процессов управления (Раздел 4.3.2 учебника "Планово-экономическое управление"), страница 3

Учитывая, что дисперсия сигнала на выходе эталонного прибора так же аддитивна, в силу линейности преобразования , где  - дисперсия сигнала на выходе эталонного прибора, когда на его вход воздействует только полезный сигнал X(t),  - дисперсия выходного сигнала эталонного прибора, когда на его вход воздействует только помеха П(t), получим, что относительная среднеквадратическая составляющая погрешности  имитационного моделирования процесса измерения  равна [12]:

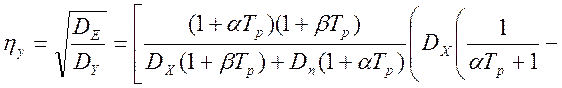
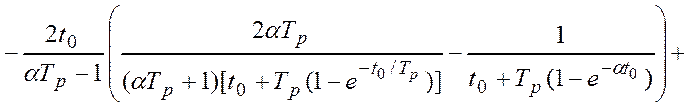
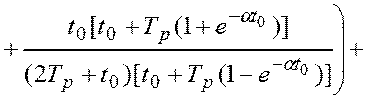
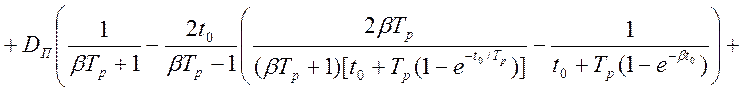
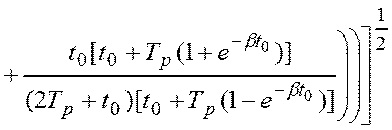.                        (4.42)

          Выражение (4.41) позволяет, при заданном шаге дискретизации t₀ =∆t=1, рассчитать значение относительной среднеквадратической погрешности цифрового моделирования аналогового эталонного прибора с весовой функцией 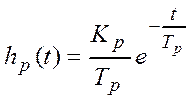 при воздействии на его вход сигнала, представляющего собой сумму двух некоррелированных стационарных случайных процессов с корреляционными функциями  и .

       Проверка адекватности математических моделей погрешности имитационного моделирования осуществлялась путем сопоставления результатов, получаемых расчетом по математической модели с результатами эксперимента на стенде [9].  Вывод об адекватности математической модели был сделан на основе сравнения значений математического ожидания и дисперсии случайной последовательности E[k,x] функции погрешности, рассчитанных по математической модели, с оценками, полученными расчетом по экспериментальным реализациям [12].

          Проверка соответствия математического ожидания , рассчитанного по математической модели, оценке , вычисленной по результатам эксперимента на стенде, осуществлялась с помощью  t- критерия : 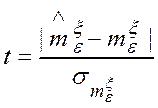, где  - среднеквадратическое отклонение оценки  математического ожидания. Значение  равно:

                                    .

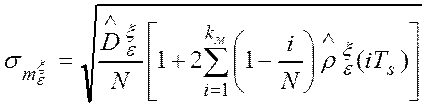Вычисленное значение tсравнивалось с табличным t_q,n для распределения Стьюдента при уровне значимости риска qравном 0.05 и числе степеней свободы n, рассчитываемом по формуле: 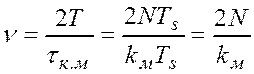, где N – длина массива составляющих случайной последовательности E[k,x], k_м– значение аргумента нормированной корреляционной функции случайной последовательности E[k,x], при котором 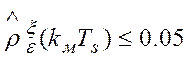. Во всех экспериментальных реализациях  t < t_q,n, , то есть оценка математического ожидания  отличается  от оценки математического ожидания  несущественно. А математическая модель [4.42] адекватна по математическому ожиданию.           Проверка адекватности математических моделей по дисперсии осуществлялась с помощью критерия F (Фишера). Для этого вычислялось отношени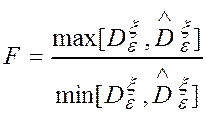е: , где 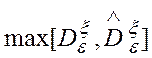,  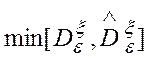- соответственно, максимальная и минимальная из дисперсий. Вычисленное значение F сравнивалось с табличным  F_табл  при уровне значимости риска равном 0.05 и числе степеней свободы равном бесконечности для  дисперсии  и числе степеней свободы  равным n ,   для оценки   вычисленной по результатам имитационного моделирования. Во всех экспериментальных реализациях  F < F_табл,  то есть различие между дисперсиями  и  можно считать несущественным, а метрологические характеристики (4.37) -:- (4.42) адекватно описывают механизмы возникновения погрешностей в аналого-цифровом преобразователе в зависимости от времён дискретизации T_С  и T_S. Время дискретизации при моделировании t₀ принималось  равным 1секунде. Аналог этого времени, в  измерительных подсистемах робастных систем, носит название время измерения, T_C. Величина этого времени полностью определяется техническими данными АЦП, а погрешности относятся к инструментальным и определяются, в основном, разрядностью АЦП.  Второе время дискретизации – это темп обработки информации в программно-аппаратном измерительном канале, T_Sназываемое в измерительной технике периодом опроса датчиков. На одном периоде опроса датчиков, должно быть целое число интервалов измерения, то есть Ts = k·Tc .