Методические ошибки моделирования процессов управления (Раздел 4.3.2 учебника "Планово-экономическое управление"), страница 4

          Модели погрешностей имитационного моделирования процессов измерения имеют, также, большое значение при автоматизированном проектировании виртуальных приборов, поскольку дает возможность количественно оценить оптимальное время измерения Т_C=t₀ , обеспечивающее минимум относительной методической динамической погрешности цифрового моделирования аналоговых динамических  преобразователей информации. Как следует из моделей метрологических характеристик (4.37) -:- (4.42) значения коэффициентов усиления первичного K_p и нормирующего K_n преобразователей, а также величина шага квантования по уровню q влияют только на составляющую общей погрешности цифровой обработки измерительной информации, обусловленную квантованием по уровню в АЦП. На практике эта составляющая пренебрежимо мала по сравнению с погрешностями от квантования по времени. Это можно показать на следующем примере [Д]. Так как значения нормального стационарного случайного процесса,  X(t)  с вероятностью 0.997  расположены в интервале, равном  и расположены симметрично относительно математического ожидания. (т.е. , где x_max, x_min - верхняя и нижняя границы диапазона изменения измеряемой величины, D_x- дисперсия измеряемой величины).

Дисперсия сигнала на входе АЦП в случае помехи с экспоненциальной корреляционной функцией будет равна [12]: 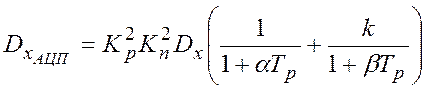, а в случае помехи типа белый шум: .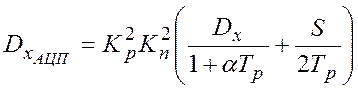

         Таким образом, в первом случае диапазон изменения сигнала на входе АЦП равен: 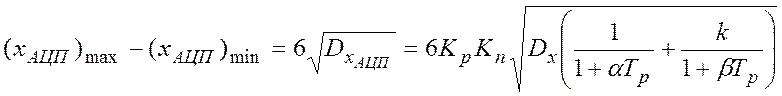, а во втором случае равен: .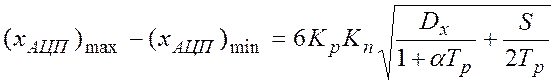

          Учитывая, что длина шкалы квантования по уровню n-разрядного АЦП равна  , должно выполняться неравенство: .Откуда, ,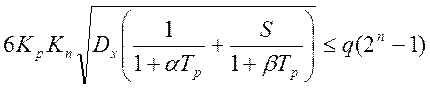

в случае помехи с экспоненциальной корреляционной функцией и, 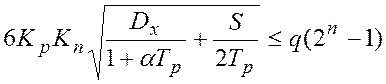, в случае помехи типа белый шум.

        Ошибка квантования по уровню будет тем меньше, чем ближе значения, получаемые в левых частях неравенств к значениям, получаемым в правых частях, и будет минимальной при значениях параметров, обращающих неравенства  в равенства. Из последней формулы видно, что существует настроечный коэффициент, T_p(постоянная времени эталонного аналогового динамического преобразователя), при котором погрешность моделирования принимает минимальное значение. Это связано с тем, что при определенной инерционности датчик эталонного прибора, выполняя функции предварительного аналогового фильтра, наилучшим образом отфильтровывает помеху. Увеличение уровня шума, S можно компенсировать увеличением значения постоянной времени первичного преобразователя, T_p . Кроме того,  постоянной времени, T_p , можно подстраиваться под единый темп обработки информации в измерительной подсистеме, T_S . Чем меньше инерционность датчика эталонного прибора, тем реже его можно опрашивать.  При небольших уровнях  помехи (S£ 0.05) уже сравнительно малая инерционность датчика эталонного прибора практически обеспечивает фильтрацию помехи, избавляя от необходимости использования специальных фильтров. В практике имитационного моделирования одинаковое значение имеет как равномерная дискретизация, так и восстановление. При этом, операция восстановления осуществляется без погрешности при условии, что период квантования по времени T_s, как основной настроечный коэффициент ЦАП в программно-аппаратном измерительном канале,  кратен шагу дискретизации T_С,  как основного настроечного коэффициента АЦП, то есть  T_S=k·T_C, где k- целое число. Учитывая этот факт, а также имеющееся ограничение на возможные значения t₀ , обусловленное обеспечением заданной точности программной реализации аналогового динамического преобразователя, значение шага дискретизации t₀ рекомендуется подстраивать, под используемый для моделирования АЦП: 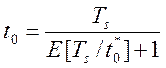, где  -  время дискретизации, которое обеспечивает минимум погрешности обработки информации. Для 8-разрядного АЦП этот минимум достигается при  0.0025 секунд (см. рис. 4.12 [9]). При этом,  дисперсия абсолютной погрешности обработки измерительной  информации равна 1.237·10 ^-10  единиц измеряемого параметра в квадрате [9].