Метрологические характеристики адаптивного управления (Раздел 4.3 учебника "Планово-экономическое управление")

            4.3  Метрологические характеристики адаптивного управления

Как было показано выше, в свойствах эталонного переходного процесса  (линия-1 на рисунке 4.7), в свойствах переходного процесса, полученного в результате имитационного моделирования процессов управления  (линия-3 на рисунке 4.7) и в свойствах оптимального переходного процесса (линия-2 на рисунке 4.7) сосредоточена вся информация о метрологических характеристиках адаптивного управления. К ним относятся методические погрешности линеаризации критериев управления, методические ошибки моделирования процессов управления и методические погрешности  текущей идентификации.

4.3.1 Методические погрешности линеаризации критериев управления

Как было показано выше, уравнение измерения текущего значения критерия управления в реальном масштабе времени имеет вид [54]:

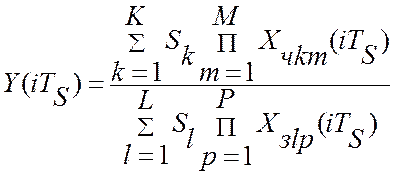
В обобщенном уравнении измерения критерия управления    K – это количество измеряемых текущих значений технологических параметров Х_чkm(iT_S)   в числителе уравнения измерения,   М – это количество мультипликативно связанных текущих значений технологических параметров в k-той составляющей суммы числителя,   L – это количество измеряемых текущих значений технологических параметров X_зlp(t), в знаменателе уравнения измерения, P – количество мультипликативно связанных технологических параметров  в l-той составляющей суммы в знаменателе,    S_k, S_l – настроечные коэффициенты информационной подсистемы АСУТП.

Мультипликативное взаимодействие измеряемых сигналов, пожалуй, самое распространенное нелинейное взаимодействие параметров в технических системах. Особенно широко оно используется в теплоэнергетике, нефтяной и газовой промышленностях, где обобщенные критерии управления имеют уравнение измерения в виде суммы произведений информации об информационных потоках: 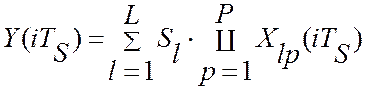   где P – количество мультипликативно взаимодействующих измерительных сигналов,  L – количество потоков обрабатываемой информации в уравнении измерения,  Х_lp(t) –  p-тый измерительный сигнал  l-том измерительном потоке,  S_l – настроечные  коэффициенты измерительных каналов,  l-того  измеряемого потока информации.

 Например, при управлении котлоагрегатом критерием управления является уравнение измерения количество генерируемого в котлоагрегате тепла:                    , где: Y₁(iT_S)- текущее значение расхода перегретого пара;  Y₅(iT_S)- текущее значение температуры перегретого пара;  intY₆(iT_S)- энтальпия перегретого пара при текущем значении давления перегретого пара.   Или, при управлении тепловыми пунктами,  критерием управления является уравнение измерения количества потребленного тепла:                              , где: Y₁(iT_S)- текущее значение расхода прямой горячей воды;  Y₂(iT_S)- текущее значение температуры прямой воды;  Y₃(iT_S)- текущее значение расхода обратной воды;  Y₄(iT_S)- текущее значение температуры обратной воды;  S₁, S₂ -  настроечные коэффициенты (энтальпия, теплоёмкость и т.д). Как видим, все критерии представляют собой сложные нелинейные функции многих переменных.  Поэтому применение этих уравнений для количественных оценок свойств систем управления требует линеаризации. Ошибка линеаризации, безусловно, влияют на точность конечной математической модели, однако ее величина может быть оценена и отнесена к методической погрешности.

       В главе 2.4 был рассмотрен  процесс линеаризации на примере мультипликативного взаимодействия N измеряемых сигналов. Текущее значение уравнения измерения, при этом ,  выражалось следующим образом [24]:

Y(iT_s)=Y₁(iT_s )· …·Y_i (iT_s )·...·Y_N(iT_s ).                        (4.28)                      

В выражении (4.28) Y₁(iT_s), Y₂(iT_s), ..., Y_N(iT_s) – текущие значения измеряемых величин в произвольные моменты времени, i·T_s. Обозначим как Y₁, Y₂, ...,Y_N – случайные величины, представляющие собой массивы значений измеряемых параметров. Сделать переход от случайной функции, Y(t)  к случайной последовательности, Y(iT_s),  позволяет, сделанный ранее [7], вывод о том, что числовая последовательность, Y(iT_s) являются стационарной. 

Линеаризация функции (4.28) обычно проводится путем ее разложения в ряд Тейлора в окрестности точки  рабочей точки   М(М₁,М₂,...,М_N), где М₁, М₂, ..., М_N  - это математические ожидания массивов случайных величин последовательности Y₁(iT_s), Y₂(iT_s) , ...,Y_N(iT_s) , с сохранением в разложении лишь членов первого порядка:

Y(Y₁, Y₂, ...,Y_N)» Y(M₁, M₂, ...,M_N)+ 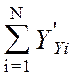(M₁, M₂, ...,M_N)(Y_i-M_i),        

где 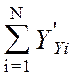 (M₁, M₂, ...,M_N ) -значения первых частных производных функции Y(Y₁, Y₂, ...,Y_N) по переменной Y_iв точке линеаризации, М_i.

Подставляя полученные производные в исходное выражение для Y(Y₁, Y₂, ...,Y_N), получается линеаризованное уравнение измерения интеллектуальной измерительной системы с мультипликативным взаимодействием измеряемых сигналов[24]:

Y(Y₁, Y₂, ...,Y_N)=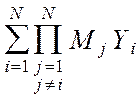- (N-1) 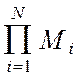                        (4.29)

Выражение (4.29) представляет собой линеаризованную в окрестности точки М функцию  Y(Y₁, Y₂, ...,Y_N) и, именно, это выражение должно использоваться при анализе и синтезе информационно-измерительной системы. Таким образом, мультипликативное взаимодействие измерительных каналов  представлено как аддитивное  и обобщенная структура линеаризованной информационно-измерительной системы будет иметь вид, представленный на  рисунке  4.8.  Из схемы видно, что замена мультипликативного взаимодействия каналов, в рамках информационно-измерительной системы, на аддитивное,  сопровождается появлением в структуре каждого измерительного канала дополнительного  звена, характеризующегося весовой функцией h_i1(t).