Метрологические характеристики адаптивного управления (Раздел 4.3 учебника "Планово-экономическое управление"), страница 4

                 Взаимокорреляционная функция показаний линеаризованной эталонной и линеаризованной программно-аппаратной измерительных систем, при типовом наборе элементов измерительного канала, будет равна [24]:

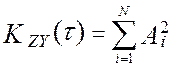
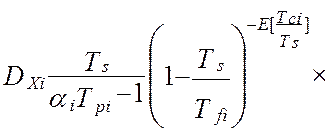
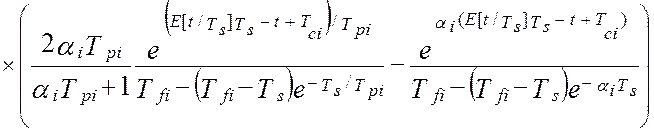    (4.35)

Принципиальной особенностью метрологической характеристики (4.35) является зависимость взаимокорреляционной функции   от текущего момента времени t =T_s -T_с, которое является случайной величиной с равномерным законом распределения [7]. Это время характеризует несовпадение текущего момента времени измерения в АЦП с текущими моментами дискретизации случайного процесса (см. рисунок 3).  Необходимо отметить, что в качестве аргумента функции  удобнее использовать не текущее время t, а величину t=t - E[t/T_s]T_s  (Е- это операция взятия целой части), которая не обращается в ноль вследствие не кратности (в общем случае) текущего значения реального времени t величине периода опроса датчика T_s .

         Таким образом, несмотря на то, что  показания линеаризованного виртуального прибора являются нестационарным случайным процессом, последовательность показаний линеаризованного виртуального прибора остается стационарной. А, следовательно,  процесс линеаризации критерия управления, методом  разложения в ряд Тейлора,  не значительно искажает вероятностные свойства измерительной информации. А величина относительной методической динамической составляющей погрешности измерения  управляющего воздействия зависит, в основном, от положения рабочей точки в пространстве управляющих координат (см. 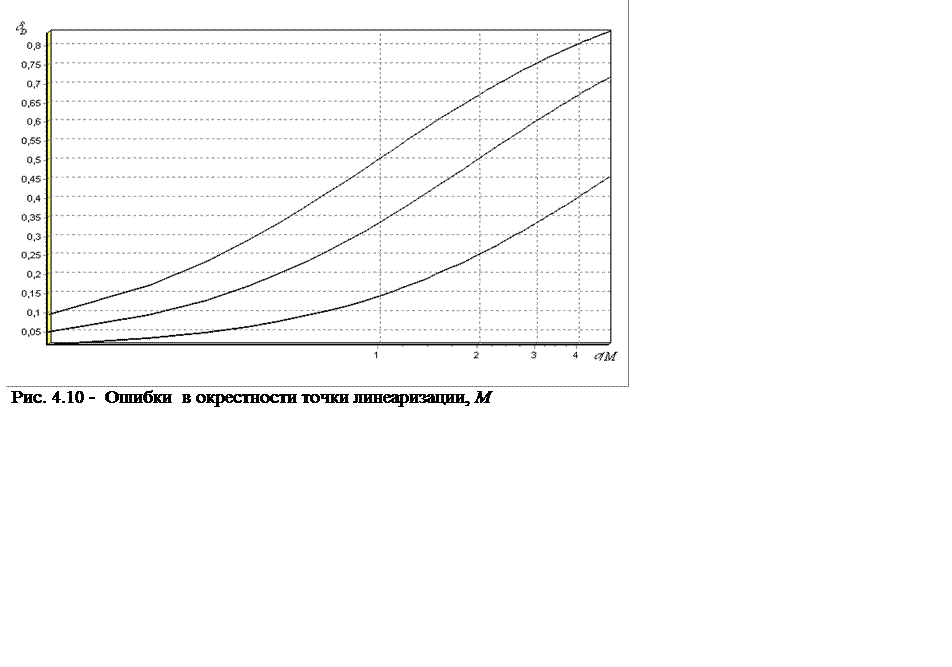Рис.4.10 и  [24]). На рисунке 4.10: 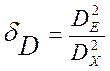. Это графики зависимости относительной погрешности линеаризации d_D от основных статистических оценок сигналов, входящих в уравнение измерения. К ним, в первую очередь относятся математическое ожидание, дисперсия и уровень помех измерения.

Анализ графиков подтверждает сделанное ранее утверждение о том, что погрешность линеаризации уменьшается с уменьшением границ изменения аргументов линеаризуемой функции, которые однозначно определяются дисперсией перемножаемых сигналов.  Чем меньше отношение среднеквадратичного отклонения сигнала к его математическому ожиданию, тем меньше становится относительная погрешность линеаризации.

Анализ свойств многих промышленных сигналов в условиях установившихся режимов технологических процессов показал, что они характеризуются небольшими колебаниями относительно математического ожидания (не более 10 %), что позволяет применить полученные математические модели ошибок, возникающих в процессе  линеаризации уравнений измерения критериев управления, для проектных и научно-исследовательских работ.

          Возникает вопрос о допущения при линеаризации случайной функции Y(t) разложением в ряд Тейлора. Это , в первую очередь, касается обоснования возможности перехода от оценок эталонного переходного процесса M_Yi, и D_Yi  к статистических характеристикам случайных функций M_Zi(t) и D_Zi(t). Учитывая, что линеаризации подвергается статическая характеристика объекта управления, а следовательно, значения измеряемых величин на выходе эталонной модели объекта управления зависят только от мгновенных значений управляющих параметров и не зависят от своих значений в предшествующие или последующие моменты времени, а также принимая во внимание тот факт, что сечение случайной функции в некоторый момент времени t представляет собой обычную случайную величину, линеаризацию функции от множества случайных функций следует признать эффективной.