В модели (4.30): Ai ,Aj – настроечные коэффициенты измерительной системы (являются функциями коэффициентов линеаризации уравнения измерения и коэффициентов статических характеристик датчиков информации); TS – единый период опроса датчиков измерительной системы; Tfi – постоянные времени программных динамических преобразователей; Tpi – постоянные времени динамических характеристик датчиков; αij – квадратная матрица скоростей изменения измеряемых величин; E[t/TS] – дискретное время (операция взятия целой части числа); Sij – матрица помех измерения; DXij– корреляционная матрица измеряемых сигналов при t=0, в которой диагональные элементы –это дисперсии измеряемых сигналов, все остальные элементы матрицы - это коэффициенты корреляции показаний датчиков.
При этом, вероятностные
свойства показаний эталонной измерительной системы полностью определяются
вероятностными свойствами измеряемых сигналов X1(t), X2(t), ..., XN(t) и динамическими характеристиками эталонных
измерительных каналов: 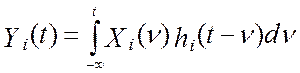 , где
hi(t) – весовая функция i-го
эталонного канала. В том случае, когда канал состоит из нескольких
последовательно соединенных звеньев, его весовая функция равна свертке весовых
функций составляющих его звеньев. Поэтому показания линеаризованной эталонной
измерительной системы будет равно сумме показаний эталонных измерительных
каналов:
, где
hi(t) – весовая функция i-го
эталонного канала. В том случае, когда канал состоит из нескольких
последовательно соединенных звеньев, его весовая функция равна свертке весовых
функций составляющих его звеньев. Поэтому показания линеаризованной эталонной
измерительной системы будет равно сумме показаний эталонных измерительных
каналов: 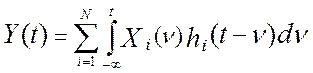 , а
Математическое ожидание показаний линеаризованного эталонного прибора, Y(t) будет
равно сумме математических ожиданий истинных значений измеряемого параметра:
, а
Математическое ожидание показаний линеаризованного эталонного прибора, Y(t) будет
равно сумме математических ожиданий истинных значений измеряемого параметра:
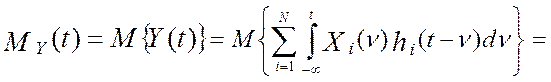
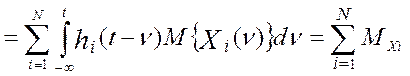 (4.31)
(4.31)
а дисперсия показаний линеаризованного эталонного прибора, Y(t) будет равна сумме дисперсий истинных значений измеряемых параметров:
![]()
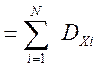 (4.32)
(4.32)
Анализ метрологической характеристики (4.32) показывает, что дисперсия показаний эталонной измерительной системы не зависит от реального времени. Следовательно, при стационарных входных воздействиях на измерительную систему показания эталонной линеаризованной измерительной системы являются стационарным случайным процессом.
Вероятностные свойства показаний линеаризованного виртуального прибора, Z(t), зависят не только от свойств аналоговых элементов измерительной системы. В большей степени они зависят от свойств программного обеспечения виртуального прибора [58]:
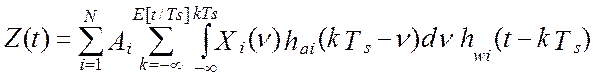 .
.
На показания виртуального прибора (9) влияют коэффициенты линеаризации (Ai), количество измерительных каналов (N), темп обработки информации (Ts), динамические свойства аналоговой части каждого программно-аппаратного измерительного канала виртуального прибора (hai), а так же динамические свойства программного обеспечения каждого программно-аппаратного измерительного канала (hwi). При этом математическое ожидание показаний линеаризованного виртуального прибора будет равно:
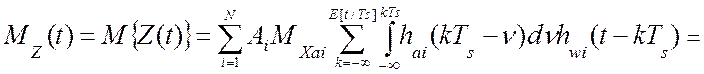
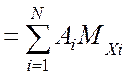 (4.33)
(4.33)
Дисперсия показаний линеаризованного виртуального прибора, при типовом наборе элементов измерительного канала, будет равна [24]:
![]()
![]()
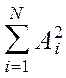
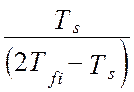
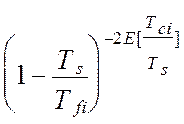 ´ (4.34)
´ (4.34)
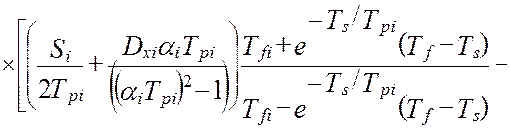
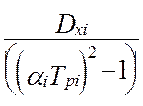
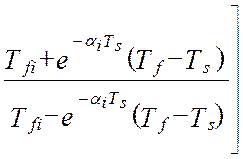
Анализ этой метрологической характеристики показывает, что даже при стационарных изменениях истинного значения измеряемой величины, Xi(t), показания виртуального прибора являются нестационарным случайным процессом. Это видно из того, что метрологическая характеристика (4.34) является функцией реального времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.