Метрологические характеристики адаптивного управления (Раздел 4.3 учебника "Планово-экономическое управление"), страница 2

Весовая функция каждого линейного динамического звена позволяет выразить показания эталонной измерительной системы , Y(t),  через показания эталонных измерительных каналов Y_i(t) :

.            

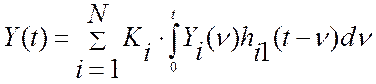Весовая функция, h_i1(t), дополнительно появляющегося звена, представляет собой безынерционное звено и определяется следующим образом:

h_i1(t)=,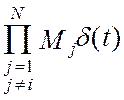                                         

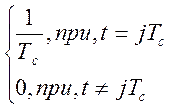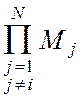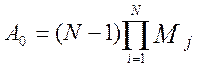где d (t)=  - весовая функция аналогоцифрового преобразования,  _jТ_с – время измерения j-того значения измеряемой величины,  1/Т_с - быстродействие АЦП (частота дискретизации измерительного процесса). Введя обозначение:  A_i=, можно весовую функцию дополнительно появляющегося звена записать в виде: h_i1(t)=A_id(t). Отсутствие в системе, (см. рис. 4.8),  сигнала  , в схеме обработки информации,  приводит к тому, что реакция линеаризованной системы на некоторое совокупное входное воздействие Y₁(t), Y₂(t), ..., Y_N(t) будет отличаться по математическому ожиданию от реакции исходной системы на такое же воздействие  на величину этого сигнала.

 

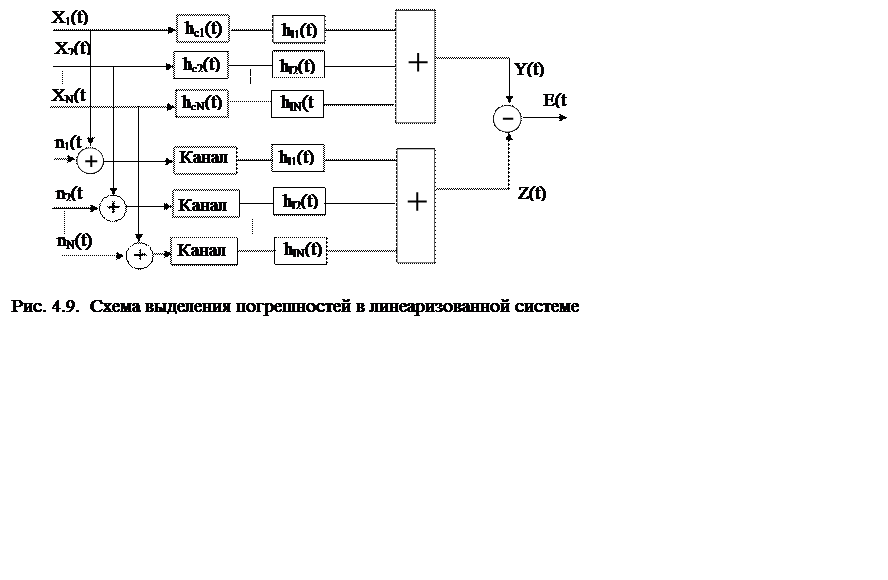
              Схема  выделения погрешности  измерения в линейной многоканальной измерительной системе представлена на рис. 4.9.  На этой схеме  Xi(t)  - измеряемые сигналы,  n_i(t)  -помехи,  аддитивно накладываемые на полезный сигнал в каждом из измерительных каналов, h1_i(t) - весовые функции дополнительных звеньев, появляющихся в структуре каналов вследствие операции линеаризации, h_ci(t) - весовые функции эталонных приборов.

            Погрешность измерения представляет собой функцию E(t), определяемую как разность между значениями технико-экономического показателя,   измеренного виртуальным прибором (программно-аппаратная измерительная система)   и эталонной  измерительной системой:

                                                E(t)=Z(t)-Y(t).

Так как и входное воздействие на измерительную систему, и ее реакция на это воздействие являются случайными функциями, то очевиден вывод о том, что и функция ошибки E(t) также является случайной функцией. Поэтому, для количественной оценки погрешности, необходимо вычислить характеристики  случайной функции E(t).

Математическое ожидание функции ошибки равно, по определению: .  Поэтому, на основании  анализа схемы обработки информации, моделей типовых элементов программно аппаратного измерительного канала и допущения о стационарности случайного измерительного сигнала математическое ожидание  функции ошибки будет равно нулю [64]:

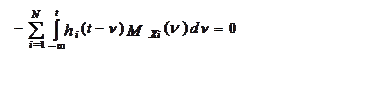
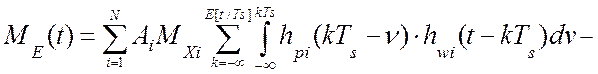Дисперсия ошибки  по определению равна [34]:

                                   ,                        

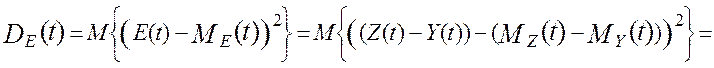
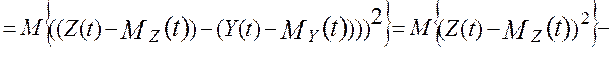
Таким образом, дисперсия методической динамической составляющей  погрешности виртуального прибора от линеаризации полностью определяется тремя основными метрологическими характеристиками измерительной системы –  это  дисперсией показаний виртуального прибора, D_Z(t), дисперсией показаний эталонной информационно-измерительной системы, D_Y(t) и взаимокорреляционной функцией этих показаний , K_ZY(t,t).  В работе [24] получена модель методической динамической погрешности измерения виртуального прибора с N измерительными  каналами при мультипликативном взаимодействии сигналов. Модель раскрыта через настроечные коэффициенты  виртуального прибора при допущениях о стационарности измеряемых сигналов и безинерционной передачи информации в эталонной измерительной системе [24]:

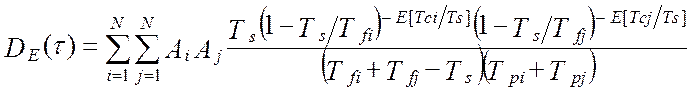
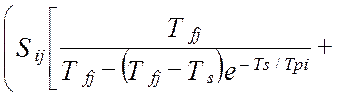
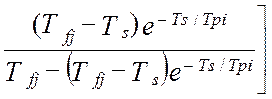
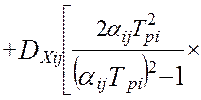
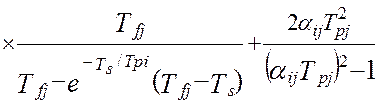
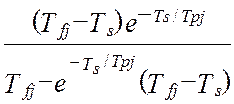
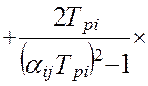
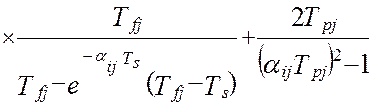
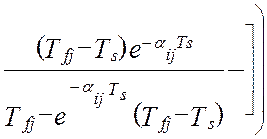
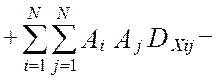
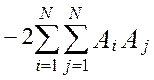
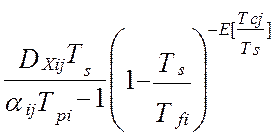
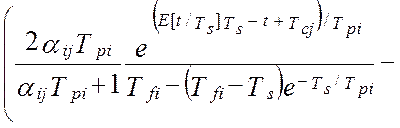
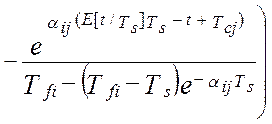                                          (4.30)