Глава 2
Математическое обеспечение робастных систем
Как было показано в главе 1, при создании робастных систем существует группа метрологических характеристик, которые характеризуют методические ошибки, возникающие в процессе проектирования системы управления. К ним относятся ошибки идентификации (см. рис.1.12), ошибки метода линеаризации критерия управления (см. рис. 1.13) и ошибки имитационного моделирования (см. рис.1.14). Таким образом, при анализе результатов проектирования робастных систем необходимо просматривать все три типа моделируемых переходных процесса (см. рис. 2.1.). Конечно же, главный – это эталонный переходный процесс (см. жирную линию-1 на рисунке 2.1), как цель которую необходимо достигнуть в процессе управления. Линия 3 на рисунке 2.1 – это переходный процесс, полученный в результате имитационного моделирования процессов управления по заданному(спроектированному) алгоритму управления. Пунктиром 2 на рисунке 2.1. показан переходный процесс, полученный в результате имитационного моделирования процесса управления при оптимальных настройках всех алгоритмов системы.
|
|
Рис. 2.1 Прогнозируемые переходные процессы
Исходным для анализа причин возникновения ошибок цифровой обработки и передачи на расстояние измерительной информации является теория потенциальной помехоустойчивости академика Котельникова В.А. [18], которая базируется на уравнении передачи дискретных сообщений:
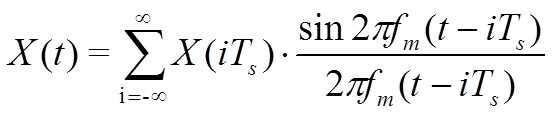 (2.1)
(2.1)
Здесь Ts – это период опроса датчиков измерительной информации о непрерывной измеряемой функции X(t) ; X(iTs) – решетчатая функция, где i – это порядковый номер измерения, fm,- частота среза или ширина спектра измеряемого сигнала, X(t).
Выражение (2.1) показывает, что любую функцию X(t), образованную колебаниями частот, лежащих в пределах от 0 до fm, можно передавать при помощи ее значений, периодически отсчитываемых с интервалом Ts = (2fm)-1 секунд. Соотношение (2.1), наряду с обеспечиваемой им математической интерпретацией процесса дискретной передачи, в виде разложения исходной функции по ортонормированным функциям, определяет и структуру основного физического процесса преобразования непрерывной функции времени при дискретной передаче информации. Эта структура состоит из операций периодического отбора мгновенных значений X(t), с последующим восстановлением по ним желаемой непрерывной функции. Класс рассматриваемых функций определен условием ограниченности их спектра полосой частот [0 – fm]. Ограничение спектра является допущением, позволяющим построить строгую модель идеальной дискретной передачи непрерывных функций. Действительно, если обозначить мгновенные отсчеты исходной непрерывной функции через X(iTs), а саму непрерывную функцию через X1(t). Тогда, в случае, когда спектр функции X(t) ограничен частотой fm и частота отсчетов fS = ТS-1 удовлетворяет условию fS = 2fm, восстановленная функция, X2(t), в соответствии с (2.1) равна исходной: X2(t)=X1(t). Если эти функции имеют преобразования Фурье U1( jf ) и U2( jf ), то и для них выполняется условие равенства спектров:
U1( jf ) = U2( jf ) (2.2)
Это соотношение позволяет не только в удобной форме анализировать свойства процесса цифровой передачи и обработки непрерывных функций времени, но и понять возможные причины нарушения равенства (2.1) и дать им соответствующую геометрическую интерпретацию [7].
Одной из причин появления систематической методической динамической погрешности реализации уравнения (2.1) связана с усечением ряда дискретных значений. В промышленных условиях это конечная величина, N, которая тесно связана с периодом нанесения управляющих воздействий, Tу, который, в свою очередь, определяет время накопления информации для идентификации эталонной математической модели. Случай восстановления функции по ее отсчетам на ограниченном (может быть, ''скользящем'' при текущей идентификации) отрезке времени представляет значительный интерес в связи с важностью повышения (при контроле и управлении) оперативности получения требуемых сведений об объекте управления и особенно при адаптивном управлении. Эту составляющую потерь информации обозначим, через ∆3 . Вторая, пожалуй, самая маленькая составляющая систематической методической динамической погрешности численной реализации уравнения (2.1) связана с измерением непрерывной случайной функции имеющей неограниченный частотный спектр. А таковыми являются все измерительные сигналы, и входные в объект управления - X(t), и критерии управления - Y(t), и возмущающие переменные- F(t) хотя бы потому, что являются случайными функциями времени из-за наложенной на них помехи измерения. Эту составляющую погрешности цифровой обработки информации обозначим за ∆2 .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.