Математическое обеспечение робастных систем (Глава 2 учебника "Планово-экономическое управление"), страница 4

       На рисунке 2.13 изображена обобщенная структурная схеме программно-аппаратного измерительного канала: G(t) – сигнал с помехой на входе в программно-аппаратный измерительный канал, Z(t) – выходной сигнал программно-аппаратного измерительного канала (результат измерения), h_a(t) – эквивалентная весовая функция аналоговой части канала,  – эквивалентная весовая функция цифровой части канала, h_r(t) – весовая функция восстанавливающего элемента (ЦАП),  – ошибка квантования по уровню в аналого-цифровом преобразователе.

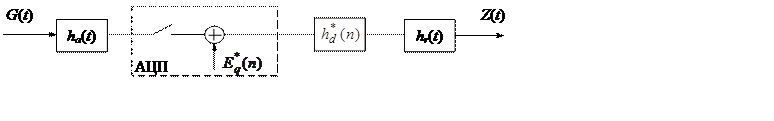
Рис.2.13 Структура программно-аппаратного измерительного канала [64]

Первая часть эквивалентной схемы операции аналого-цифрового преобразования (рис. 2.13) – это E_q(t) – часть помехи, вызванная эффектом квантования по уровню тесно связана со случайной фазой процесса измерения и поэтому  близка, по своей природе, к физическому белому шуму .

      Если применить модель отбора измеренных значений из нестационарного случайного процесса в виде: 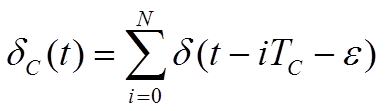      , то  измеряемый сигнал X(t) преобразуется в дискретную (решетчатую) функцию: .

             Таким образом, с выхода импульсного элемента (АЦП) поступает последовательность дельта-функций. Каждая величина этой последовательности имеет вес, равный  значению квантуемого сигнала в момент квантования t=iT_C , который совпадает также с моментом выдачи импульса. Таким образом, только функция отбора 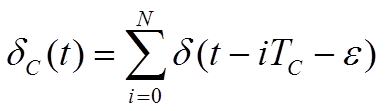обеспечивает стационарность в широком смысле случайной последовательности, получаемой из исходного непрерывного стационарного случайного сигнала. При этом, очевидно, что имеется в виду стационарность дискретного сигнала X_И(iT_C ) как функции непрерывного времени.

Линейность  операции дискретизации во времени вытекает непосредственно из главного свойства  дельта-функции [20]: 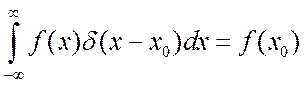                                        , согласно которому решетчатая функция X_И(iT_C ) на выходе импульсного элемента будет выражаться через входной непрерывный сигнал X(t) следующим образом:

                         

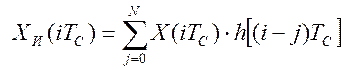
Переходя на терминологию функционального анализа, имеем:

                                 ,

где  L – линейный оператор, преобразующий функции.   

Покажем, что оператор временной дискретизации является линейным.  Пусть       . Тогда

 .

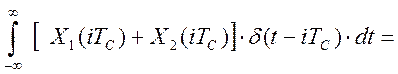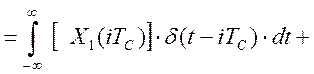
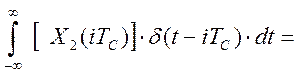
                                                               (2.7)

 То есть свойство аддитивности выполняется.

          Теперь  пусть  , тогда   .

Действительно:

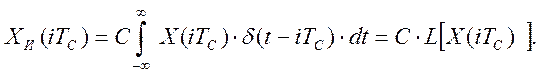                 (2.8)

По аналогии, решетчатая функция Z(iT_S) на выходе программно-аппаратного канала (см. рис. 2.13) будет выражаться через входной непрерывный сигнал Х(t) следующим образом:

                         ,

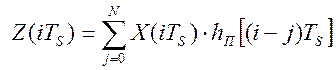 где : - это весовая функция программно-аппаратного измерительного канала.

Переходя на терминологию функционального анализа, имеем:

                                 ,

где  L – линейный оператор, преобразующей функции.   

Пусть       . Тогда

 .

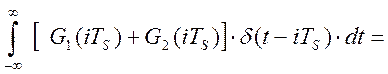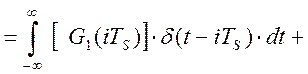
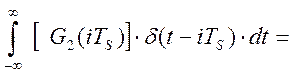
                                                               (2.9)

 То есть свойство аддитивности выполняется и для показаний регистратора хранимой информации.

          Теперь  пусть  , тогда   . Действительно: 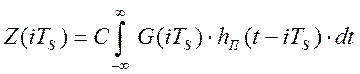, так как весовая функция программно-аппаратного измерительного канала: , является линейной операцией свертки отдельных элементов программно-аппаратного измерительного канала (см. рис. 2.13). А, следовательно:

                                                                (2.10)

Выражения (2.7) -:- (2.10) удовлетворяют определению линейного оператора, откуда следует возможность, необходимость и достаточность применения метода суперпозиции при рассмотрении задач прохождения сигналов через все элементы программно-аппаратного измерительного канала, осуществляющего временную дискретизацию и восстановление измерительной информации.

         

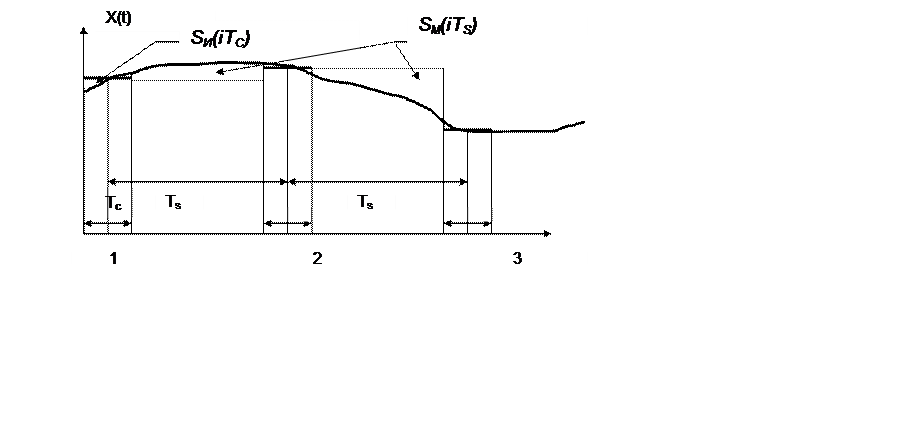
Рис. 2.14   Потери  информации при цифровой обработке   

Из рисунка 2.14 видно, что инструментальные ошибки, возникающие в процессе измерения, и которые пропорциональны площади, S_и(iT_C) много меньше методических ошибок, которые пропорциональны площади, S_M(iT_S).  Это позволяет исключить из числа параметров настройки информационно-измерительной подсистемы АСУТП время измерения, T_C , и тем самым снизить размерность задач параметрического синтеза виртуальных приборов для измерения критерия управления без существенного снижения требований к точности измерения этого критерия управления.