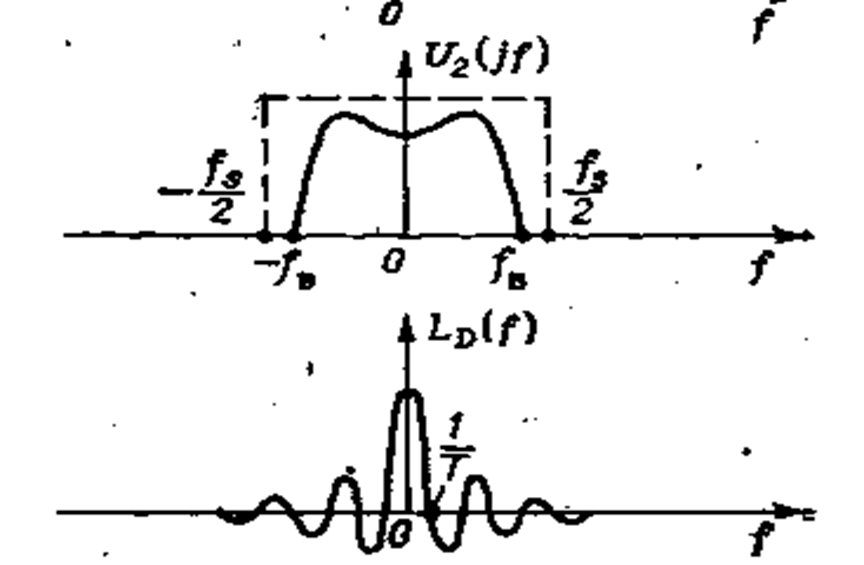
 |
Рис. 2.7 Спектр одного измерения, как результат работы АЦП
 |
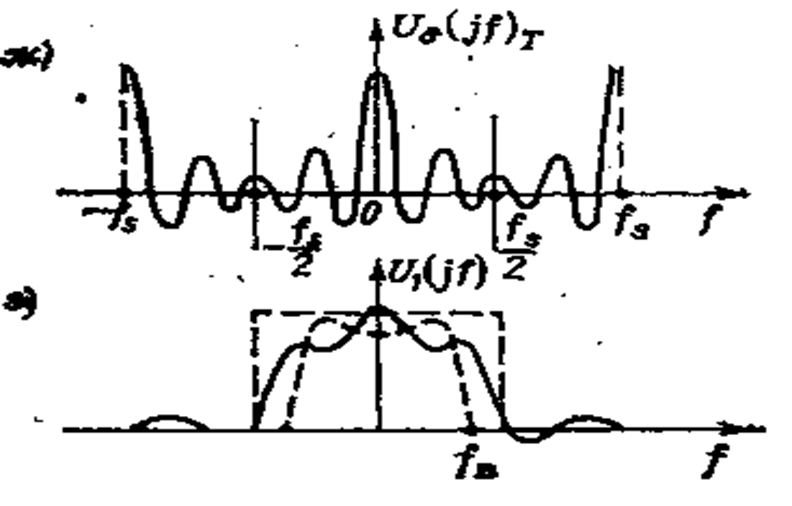Рис. 2.8. Восстановленный спектр, как результат работы ЦАП
В промышленных измерительных и управляющих системах восстанавливающий элемент – это модуль УСО для вывода аналоговой информации (регистраторы, дисплей компьютера), динамические характеристики которого целесообразно описывать восстанавливающим элементом нулевого порядка. Из рисунков 2.7 и 2.8 видно, что равенство спектров (2.2) нарушается [7] даже в случае ограниченного спектра исходного сигнал и в уравнении 2.1 появляется составляющая систематической методической динамической погрешности процесса восстановления непрерывного сигнала из дискретных значений измеряемой величины, ∆2M .
Передаточная функция модуля УСО для вывода аналоговой информации (ЦАП) имеет
вид:
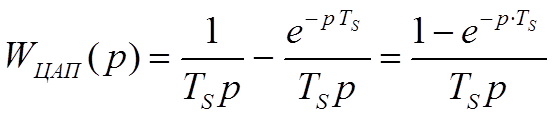
Тогда детерминированная стационарная последовательность прямоугольных импульсов регистратора (ЦАП, см. рис. 2.9) имеет вид:
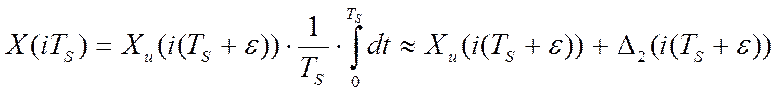
Массив хранимой информации, длинной N, запишется как:
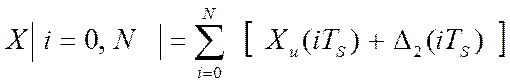(2.6)
где: ∆2 (iTS) – текущее значение погрешности измерения истинного значения измеряемой величины, X(t).
Следует обратить внимание (см. рис. 2.6), что инструментальная составляющая ошибки цифровой обработки, ∆2и , практически не изменилась, а вот методическая составляющая цифровой обработки информации, ∆2M , стала на много меньше. То есть потери информации на много сократились.
Таким образом, регистраторы (ЦАП) являются программируемыми фильтрами измерительной информации, а, следовательно, с этими потерями информации можно бороться программными методами. Использование фильтрующей способности цифровой обработки информации широко используется в информационно-измерительных подсистемах робастных систем.
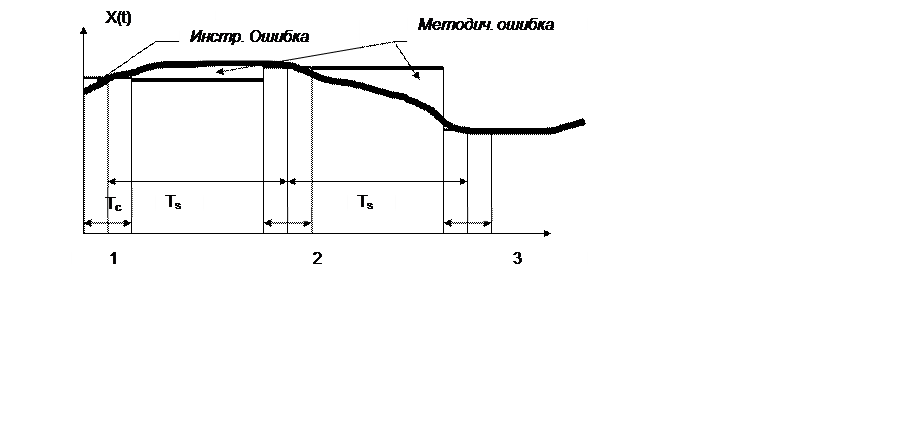
Рис. 2.9 Фильтрующая способность цифровой обработки информации
Итак, если за модель модуля УСО для вывода аналоговой информации (ЦАП) взять весовую функцию в виде прямоугольного импульса:
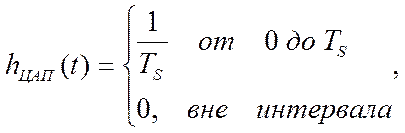
То, последовательность измеренных и восстановленных значений случайного процесса будет иметь вид непрерывной, кусочно-линейной зависимости.
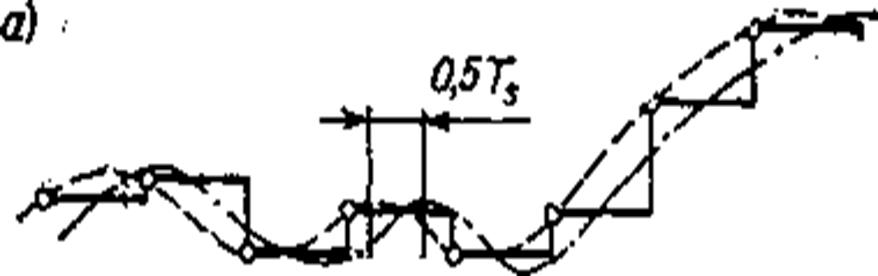
Рис. 2.10. Восстановленные (ступенька), измеренные значения(пунктир) и истинные значения измеряемой величины (штрих пунктир)
2.1.3. Свойства цифровых последовательностей
Из рисунков 2.9, 2.10 видно, что цифровая последовательность управляющего воздействия X(iTS) похожа на стационарный случайный процесс на периоде управления, TУ. Последовательность Y(iTS) так же стационарна, если время регулирования системе робастной стабилизации больше 10TР (TР – время регулирования или длина переходного процесса в системе робастной стабилизации управляющего воздействия, X(t).
Последовательность
обобщенного критерия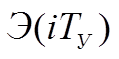 
вообще представляет
собой последовательность прямоугольных импульсов. Это позволяет прошлую, то
есть запомненную в памяти ЭВМ информацию использовать для прогноза текущих
значений выходных координат объекта управления, используя интеграл свертки
управляющего воздействия с весовой функцией объекта управления:
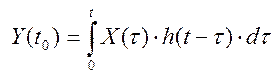
Пусть 
, а
.
Тогда, (см. рис.2.11) текущие значение критерия управления запишется, через
последовательности цифровых значений управляющего воздействия и весовой функции
объекта управления, следующим образом:
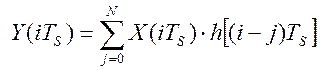
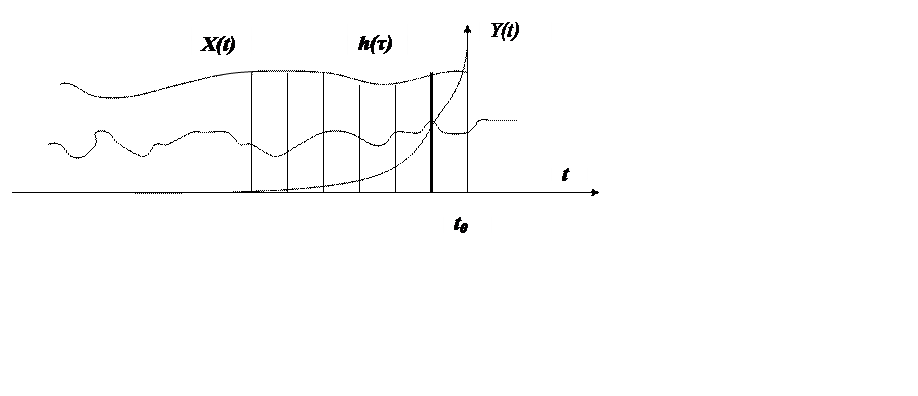
Рис. 2.11 Иллюстрация работы
алгоритма прогноза текущего значения
Аналогично, для случайных
функций, которые связаны сверткой: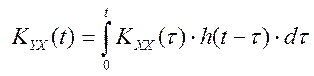 
, где KXY(t), KXX(t), h(t) – соответственно, корреляционные и
весовая функции объекта управления, цифровая последовательность
взаимокорреляционной функции будет иметь вид: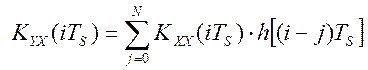 
.
При этом, 
Анализ цифровых последовательностей в робастной системе управления (см. рис. 2.12 и [6, 8, 9, 27]) показывает, что свойства показаний программно-аппаратного измерительного канала, Z(t) (см. рисунок2.13) зависят только от свойств элементов измерительного канала.
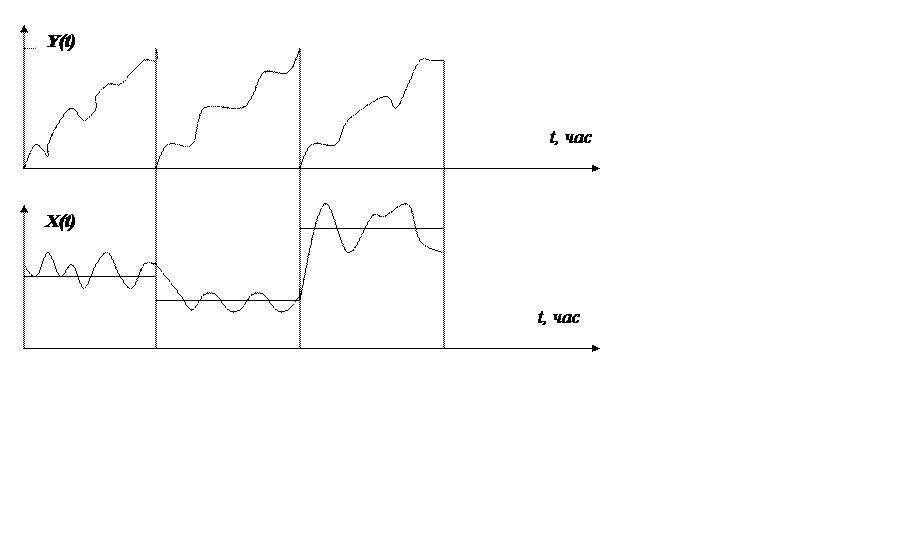
Рис.2.12. Последовательности управляющего воздействия и критерия управления в процессе адаптивного управления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.