Математическое обеспечение робастных систем (Глава 2 учебника "Планово-экономическое управление"), страница 2

   Существенные динамические влияния, характерные для крупномасштабных объектов управления,  и значительный уровень помех приводят к дрейфу оптимального режима, который должна отслеживать робастная система управления приводит к потерям информации на периоде идентификации эталонной модели, T_И. Это потери остаточного дрейфа, которые обозначим за ∆₁. Эти потери, конечно, самые большие и полностью определяются операцией регистрации измерительной информации.

   2.1 Физические основы цифровой обработки информации

                 2.1.1 Модель отбора измерительной информации

Процедура измерения сигналов (см. рис. 2.2) в робастных системах возложена на модули УСО для ввода  аналоговой информации. Наиболее простым в реализации является модуль ввода аналоговой информации, который генерирует прямоугольные импульсы малой ширины (см. рис. 2.3). Динамическое преобразование этих спектров представлено на рисунке 2.4. Это справедливо, если время измерения, Т_С  , стремится в 0.

         Таким образом,  модель процесса измерения текущих значений может быть представлена весовой функцией прямоугольного импульса:

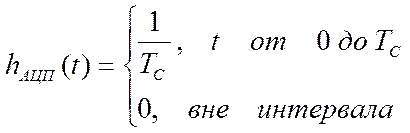             (2.3)

Передаточная функция, при этом, выглядит:

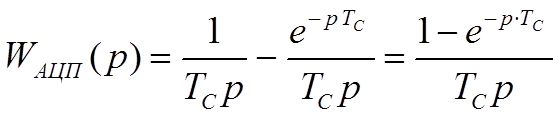
где T_С – время измерения, или время срабатывания модуля ввода измерительной информации.

.

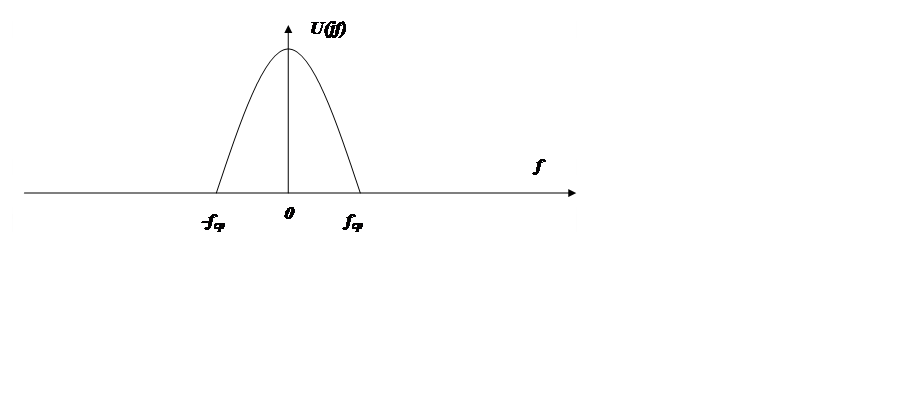
Рис.2.2  Спектр исходного измеряемого сигнала, U(jf)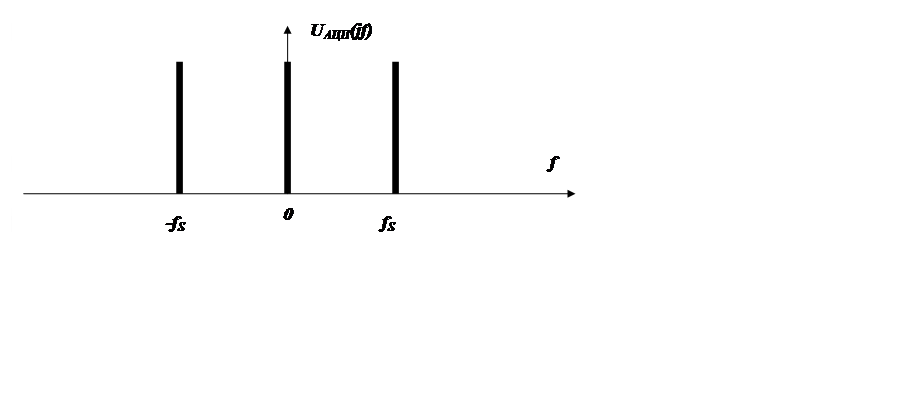                                                                                                                                                                  

Рис. 2.3  Спектр сигнала генерируемого модулем УСО (МВА),U_АЦП(jf)

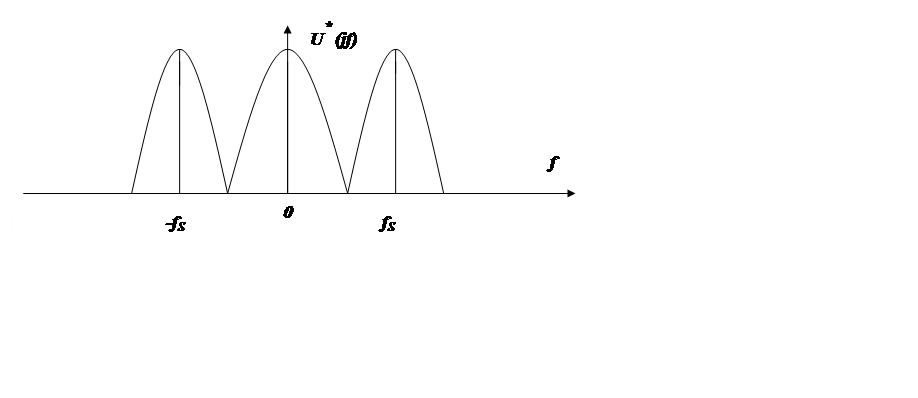
Рис. 2.4.        Итоговый спектр     U^* (jf)=U(jf)·U_АЦП(jf)  

          Ошибки, возникающие в процессе измерения, можно представить рисунком 2.5. Величина потерь информации, ∆_2и, здесь пропорциональна площади, S_и(iT_C) и относится классу инструментальных (в основном – это качество изготовления микросхем). Величина потерь информации, ∆_2M, между соседними измерениями пропорциональна площади, S_M(iT_S) и относится классу методических погрешностей. Она то и вносит наибольший вклад в общую погрешность измерения:  ∆₂   =     ∆_2и     +  ∆_2M .           

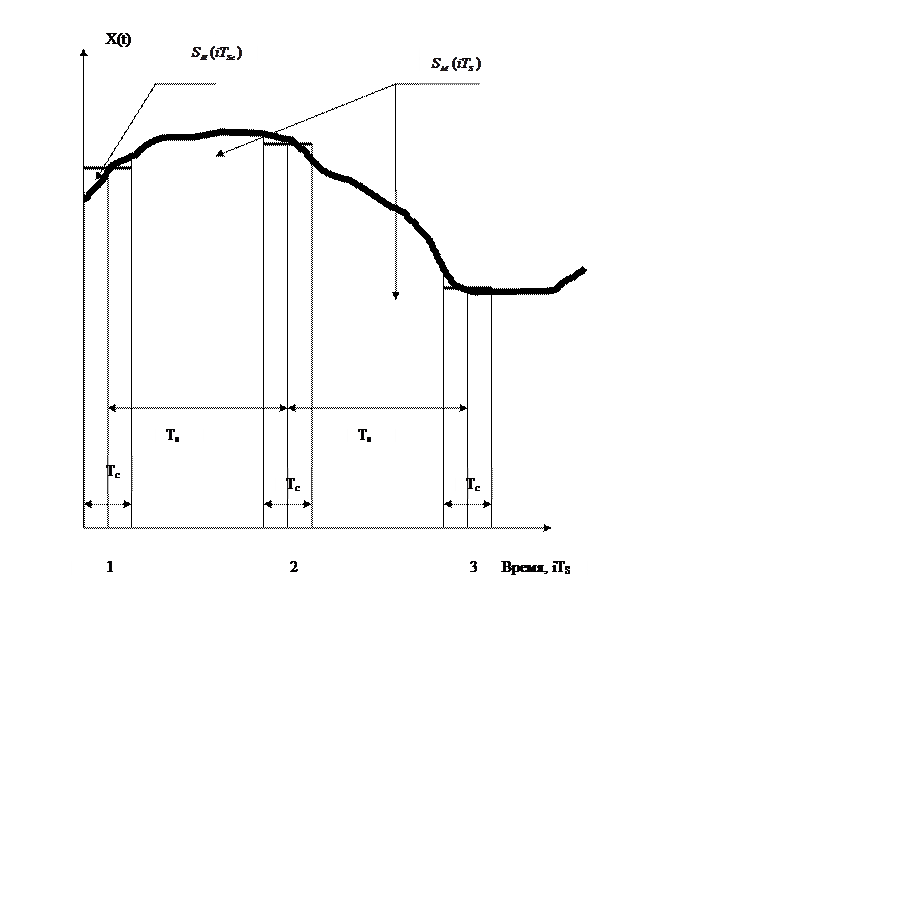
       Рис. 2.5 Физический смысл процедуры измерения (модель отбора)

Таким образом, измерительную информацию можно представить в виде последовательности прямоугольных импульсов:

                         

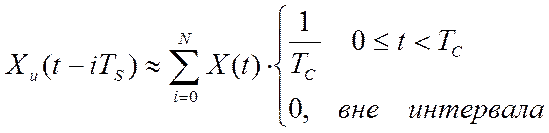
      Тогда   истинное значение измеряемой величины на выходе АЦП   имеет вид:

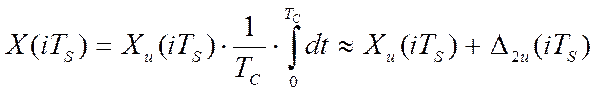                             (2.4)

где: текущее значение инструментальной составляющей погрешности цифровой обработки информации; X_и(iT_S) – текущее значение измеряемой величины на выходе АЦП.

Массив измеренной информации, длинной N, обозначим как последовательность текущих измеренных значений измеряемой величины: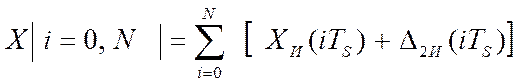. И тогда, модель процесса измерения запишется в виде последовательности прямоугольных импульсов: 

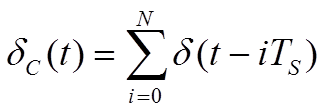                    .                                                     (2.5)

С текущим значением инструментальной составляющей погрешности цифровой обработки информации,, бороться программными методами невозможно, так как она полностью определяется величиной случайной фазы (см. рис. 2.6).

 Под случайной фазой процесса измерения будем понимать нестационарную случайную величину, 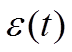 , наступления события открывания АЦП для процесса измерения (см. рис. 2.6).  Тогда, выражение (2.4) примет вид:

 

 

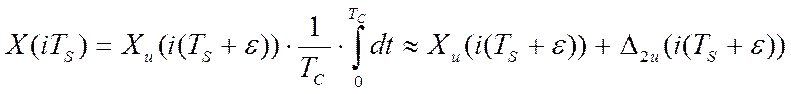
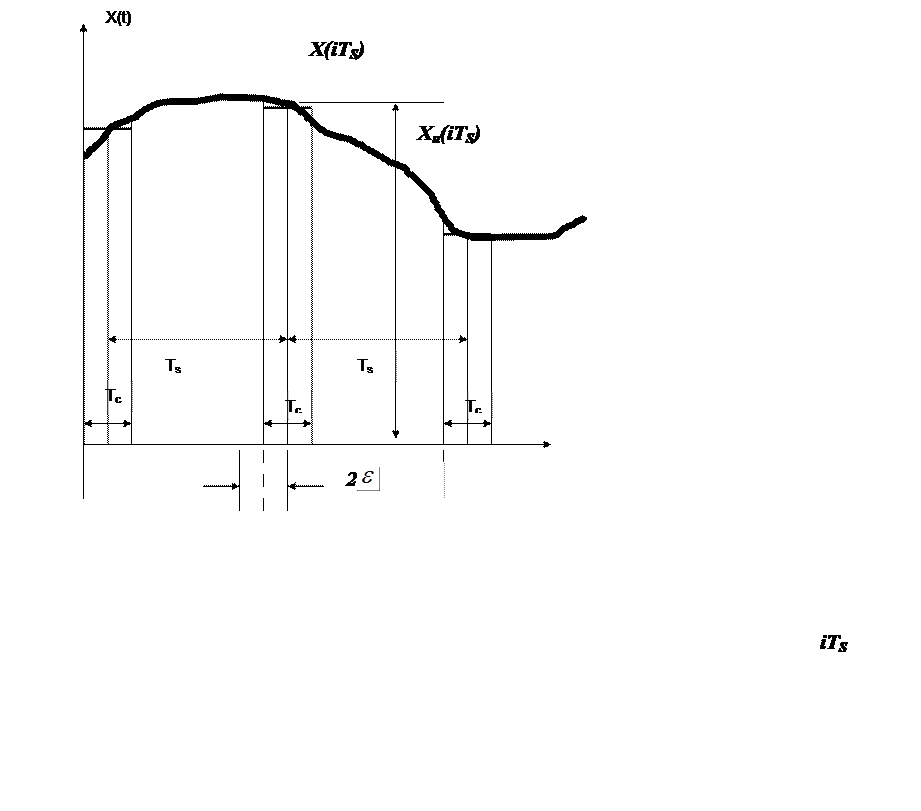Рис 2.6.  К понятию случайной фазы  процесса измерения

В работе [7] показано, что для создания условий стационарности и эргодичности последовательности текущих значений измеряемой величины необходимо и достаточно, чтобы закон распределения, f(e) имел вид:

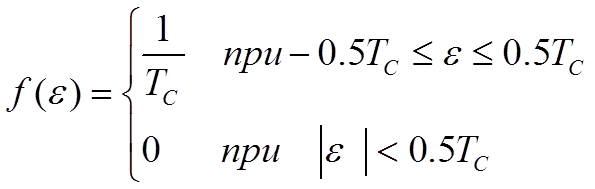
Тогда, модель отбора измеренных значений из нестационарного случайного процесса будет иметь вид:

      , 

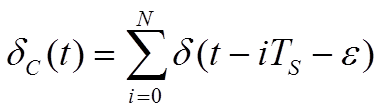где  e – случайная фаза.

          2.1.2   Модель регистрации (хранения)  измеренного значения

Восстановление аналогового сигнала по цифровым значениям, хранящимся в памяти ЭВМ - это пожалуй самая основная, причина больших потерь информации. Это связано с тем, что восстанавливающий элемент, с помощью которого осуществляется восстановление функции из дискретной последовательности отсчетов, относится к классу физически нереализуемых линейных динамических операторов и имеет весовую функцию [18]: 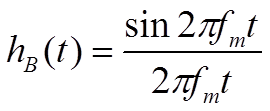.  В модели (2.1)  это представлено как результат операции свертки модели отбора (2.4)  с весовой функцией восстанавливающего элемента нулевого порядка [7]: 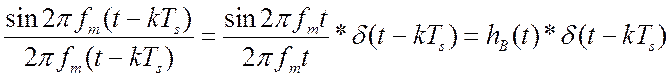              . Или в частотной области: 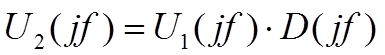, где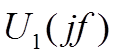 - это спектр исходного непрерывного сигнала, а 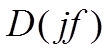 - это одна составляющая модели регистрации измеренной величины (функция-окно). На рисунке 2.7 изображена последовательность преобразования спектра исходного измеряемого сигнала, 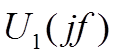, с помощью спектра функции-окна, 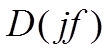 ,  в итоговый спектр одного измерения 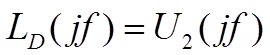. На рисунке 2.8 представлен итоговый спектр исходного сигнала, U₁(if) восстановленного по трём измерениям, U_σ(jf).