Динамика решётки. Колебания одномерной одноатомной цепочки. Теплоёмкость твёрдых тел. Модель Эйнштейна

ДИНАМИКА РЕШЁТКИ

Колебания одномерной одноатомной цепочки.

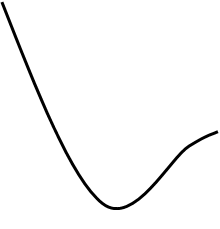
Рассмотрим бесконечную цепочку из атомов, расстояние между которыми равно а, так что равновесная координата n-го атома х_n =na. Обозначим U_n смещение n-го атома из положения равновесия. Тогда x_n=na+U_n, а изменение расстояния      

 между атомами n и n-1                                                               v

x_n= x_n-x_n-1-a=U_n-U_n-1            (1).                                                Парабола----

Разложим потенциальную энергию взаимодействия                                     

соседних атомов по степеням x                                                                                                                                                                                      

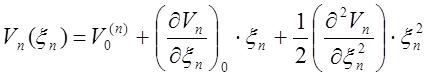     (2)

где V₀⁽ⁿ⁾- энергия взаимодействия атомов на расстоянии а.

В (2) первая производная обращается в ноль. С учётом (1) получаем

V_n=V₀⁽ⁿ⁾ +1/2a(U_n-U_n-1)²                     (3)

Здесь 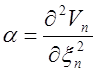 - силовая постоянная, >0

Потенциальная энергия всей цепочки V

V=SV_n=V₀+1/2×a×S(U_n-U_n-1)²             (4)

Сила, действующая на n-й атом

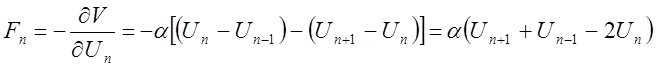
в классическом случае уравнение движения атома

             (5)

где m – масса атома. Решение будем искать в виде f

U_n=U₀×e^{-i(w×t-q×n×a)}                         (6)

т.е. в виде бегущих волн.

Колебания цепочки, при которых все атомы колеблются с одинаковой частотой, называются нормальными модами колебаний. Подставляем в (5) (6),

mw²=a(2-e^+i×q×a-e^-i×q×a)=2a[1-cos(q×а)]       (7)

учитывая, что w>0 из (7) получаем

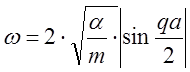         (8)

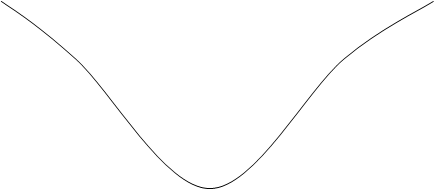 на рис2 показана дисперсионная зависимость w(q).                                    w_m

видно, что все q содержаться в интервале

-p/а<q<p/а, т.к. другие значения q сводятся к

этим. Для одномерного случая это аналог первого

закона Брилмоэна. Максимальное значение

частоты  w_max=2    Волны с частотами                  

большими w_max не могут распространяться в           -p/а                                                              p/а

такой цепочке при этом длинна волны равна l =a×а. т.е. соседние атомы колеблются в противофазе. По порядку величины w_max  10¹²с^-1

в низко частотной области 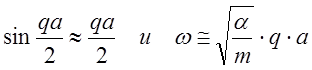                 (9)

т.е. дисперсия отсутствует.

Найдём фазовую и групповую скорости волны

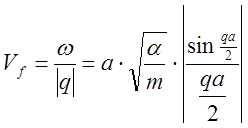                      (10)

                                                   

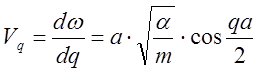
при q=0 фазовая и групповая скорости имеют одинаковые значения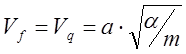

Теперь рассмотрим цепочку, содержащую конечное число атомов. Для определения движения атомов необходимо задать граничный режим, т.е. граничные условия. Если N – число атомов в цепочке очень велико, то вид граничных условий мало влияет на колебания цепочки. Часто применяют условия Борна – Кармана, представляют собой цилиндрические ,графические условия, при которых                                             U_n=U_n+N                  (11)

Из выражения (6) видно, условия цилиндричности выполняются если

е^i×q×N×a=1 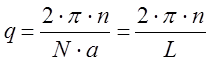        (12)

значит волновой вектор q может принимать дискретные значения, учитывая, также, что все его значения расположены внутри первой зоны Брилмоэна, такой вектор называется квазиволковым. Если N – число атомов в решётке, то число степенней свободы равное N , это как раз равно числу различных допустимых значений q.

Наиболее общее выражение вт виде суперпозиции выражений (6)

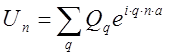       (13)

Суммирование производится по всей зоне Брилмоэна, зная набор Q_q, мы автоматически знаем U_n из (15). Т.е. величины Q_q являются также некоторыми координатами, которые называются обобщёнными. Подставляя (13) в (5) получаем

        (14)

это уравнение гармонического осциллятора. Уравнение для совокупности движения атомов  разбилось на N независимых уравнений (14). Q_q являются действительно нормальными координатами.

Чтобы уравнение (13) было действительным, необходимо, чтобы

Q_-q=Q_q^*                          (15)

Это не уменьшает количество степеней свободы, т.к. каждое Q_q определяется двумя величинами                  (R_e и I_m)  Энергия цепочки.

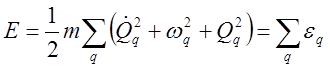    (16)

Т.е. энергия колебаний связанных атомов равна сумме энергий колебаний отдельных осцилляторов. Однако, нельзя представлять осцилляторы в виде атомов. У них общее только значение массы  m . Каждый осциллятор -  нормальное колебание калоссального числа атомов.

   В квантовом случае необходимо записать и решить уравнение Шредингера. Для совокупности осцилляторов оно имеет вид:

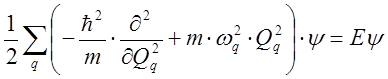       (17)

где y - в.ф. , а Е – энергия всей системы . т.к. левая часть разбивается на сумму слагаемых каждое из которых зависит только от одной переменной, то

y(Q₁,Q₂,…Q_n)=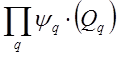              (18)

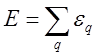                                      (19)

Из квантовой механики известно решение уравнения Шредингера для гармонического осциллятора. Значение энергии получается квантовым.

           (20)