Тепловое расширение кристаллов.
При изменении температуры кристаллы расширяются или сжимаются. Количественной
характеристикой этих процессов является объемный коэфф.
расширения 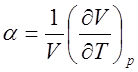 . Обычно a>0,
. Обычно a>0,
однако существует целый ряд с отрицательным значением a ( висмут, чугун, вода при 0°<Т<4°с).объём при некоторой температуре равен
![]() (1)
(1)
Можно ввести в рассмотрение и линейный коэффициент
расширения 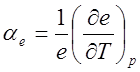 При конечной температуре.
При конечной температуре. ![]()
т.е. ![]() (2)
(2)
в случае анизотропных сред (монокристаллы) a является тензором второго ранга. Он может быть приведён к главным осям, тогда а= а1+ а2 +а3. Для кубических кристаллов a1=a2=a3 и мы приходим к (2). Обозначим
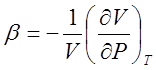 - сжимаемость. Тогда для связи a,b с теплоёмкостью существует соотношение Грюнейзена
- сжимаемость. Тогда для связи a,b с теплоёмкостью существует соотношение Грюнейзена ![]()
где Cv - теплоёмкость, g - постоянная Грюнейзена, значение которой »2 (у NaCI ==1.63 у Cu==1.96) для получения выражения a через микроскопические постоянные запишем выражение для потенциала межатомного взаимодействия с точностью до членов третьего порядка
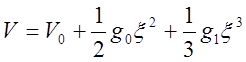 (3)
(3)
где 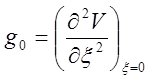
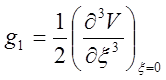 а x - отклонение положения равновесия при
Т=0.Производная от (3) по x равна силе, действующей на атом. Усредняя её и приравнивая к нулю
получим
а x - отклонение положения равновесия при
Т=0.Производная от (3) по x равна силе, действующей на атом. Усредняя её и приравнивая к нулю
получим
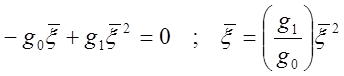 (4)
(4)
далее используем тот факт, что средняя потенциальная энергия осциллятора равна
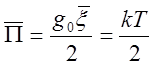 (5)
(5)
отсюда получаем 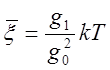 . Найдём относительное
удлинение цепочки атомов.
. Найдём относительное
удлинение цепочки атомов.
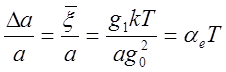
тогда 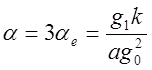 (6)
(6)
по порядку величины aе составляет ~10-5 град-1. Например (aе)Ni=1.3·10-5
Теплопроводность
Теплопроводность кристаллов обусловлена в основном двумя факторами – решёточная и электронная составляющая
![]() א=C1אреш+С2אэл
א=C1אреш+С2אэл
при описании решёточной теплопроводности используют понятие фонон – фононного взаимодействия. При таких процессах возможны рождение и уничтожение фононов. При этом выполняются законы сохранения энергии и квазиимпульса с точностью до вектора обратной решётки.
![]()
![]()
![]()
![]() +
+![]() =
=![]() +
+![]()
|

 в.в.
в.в. ![]() , направленный против
исходных векторов.
, направленный против
исходных векторов.
![]()
 Процесс переноса тепла рассматривается с позиций
переноса его в газе,
Процесс переноса тепла рассматривается с позиций
переноса его в газе,
![]() Частицами которого являются фононы
Частицами которого являются фононы
Тогда
א=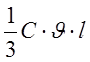
где С – теплоёмкость ,![]() - скорость звука, l –
длина свободного пробега .
- скорость звука, l –
длина свободного пробега .
При высоких температурах l определяется
Процессами рассеяния фононов на фононах и а~1/T ,
следовательно, т.к. в этом интервале С=const имеем א~1/T .
При температурах Т<![]() уже а~exp(
уже а~exp(![]() /T), א имеем такой же ход. Величина
/T), א имеем такой же ход. Величина ![]() обычно в 2¸4 раза меньше
обычно в 2¸4 раза меньше
![]() -температуры Дебоя. При очень низких
температурах С~T3 , а l имеем постоянную величину которая связана лишь с рассеянием на
дефектах. Т.о. ход зависимости א(Т) не монотонен и имеет максимум при
температуре »(1/20¸1/25)
-температуры Дебоя. При очень низких
температурах С~T3 , а l имеем постоянную величину которая связана лишь с рассеянием на
дефектах. Т.о. ход зависимости א(Т) не монотонен и имеет максимум при
температуре »(1/20¸1/25) ![]()
Кроме рассеяния на фононах, фрононы могут рассеиваться на дефектах :
1. точечных
2. линейных
3. границах зёрен в поли кристаллах и внешних поверхностях в монокристаллах.
4. Раз упорядочения в сплавах
5. Случайном распределения изотопов хим. элементов.
Электронная составляющая в теплопроводности особенно велика в металлах»95. Это объясняется большёй ролью электронов в процессах переноса. Т.к. электроны имеют заряд, то процессы теплопереноса и электропереноса тесно связаны.
Закон Видемона-Франца гласит, что при постоянной температуре отношение теплопроводности к электропроводности различных металлов постоянно. Лоренц показал, что
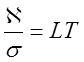
где s электропроводность , L – число Лоренца. Квантовая теория даёт выражение для L
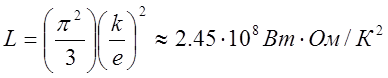
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.