Динамика решётки. Колебания одномерной одноатомной цепочки. Теплоёмкость твёрдых тел. Модель Эйнштейна, страница 3

колебаний цепочки с базисом (рис2)

существенной особенностью рис1 является наличие

области запрещённых частот для

если бы m=M, то параметр решётки бы стал а, и щель

исчезла, а мы бы пришли к

 

Трёхмерный кристалл с многоатомным базисом

В таких кристаллах также существуют продольные и поперечные волны, которые могут быть акустические и оптические. Если кристалл содержит p атомов в базисе, то всего имеется 3pN мод колебаний = числу степенней свободы, из которых

N-продольных акустических мод

2N- поперечных акустических

(p-1)N-продольных оптических

2(p-1)Nпоперечных оптических.

Дисперсионные кривые реальных кристаллов с базисом очень сложны, причём базис может быть составлен из одинаковых атомов .

На рис 1 приведён пример дисперсионных  

кривых для кристалла NaI. Все поперечные

моды двукратно вырождены ширина запрещённой

 зоны довольно большая из-за большого различия 

в массах  Na и I

 

                                                                     1/21/21/2                                           100

фононные дисперсионные кривые не зависят от температуры до тех пор пока ещё выполняется закон Гука. Однако всё же стараются их строить при низких температурах.

Плотность состояний

1)  одноатомная цепочка .

общее число состояний = N. Плотность состояний определяется (по модулю q )

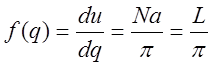          (1)

теперь запишем плотность распределения в зависимости от w :

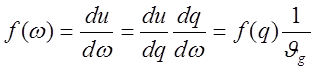
c учётом (10) и (1) получим

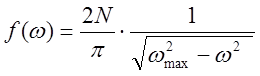    (2)

2)трёхмерный одноатомный кристалл.

Расстояние между точками в q пространстве равно 2п/L. В трёхмерном случае на каждую точку приходится объём (2п/L)³ . плотность f(q) определяется так (на 1 ед. объёма)

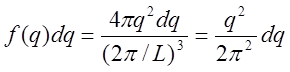     (3)

или в низко частотном приближении без дисперсии когда

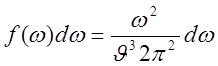              (4)

плотность поперечных колебаний в два раза больше. Общая плотность

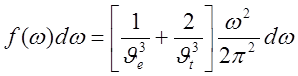   (5)

реальные плотности для кристаллов имеют гораздо более сложный вид (рис.1).

их получение представляет значительные                                  f

трудности. Значения w, при которых график имеет

 резкие  изломы, называются кристаллическими

точками, или особенностями Ван Хова. Они

зависят от разных факторов :топологии ,

поверхностей равных частот , спектров и т.д.

такие особенности есть и электронном спектре

                                                                                                                             рис.1.                            w

теплоёмкость твёрдых тел.

Классическая модель.

Теплоёмкостью называется величина

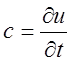       (1)

в зависимости от того, в каких условиях происходит процесс, различают теплоёмкость при постоянном давлении или объёме и обозначают соответственно С_р и С_v. Из термодинамики известно, что

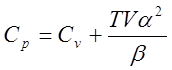                              a - коэф-нт объёмного теплового расширения.

                                                           b - изотермическая сжимаемость

и обычно для твёрдых тел разница между С_р и С_v составляет всего 3¸5%. Поэтому мы будем писать просто С.

пусть атом колеблется с частотой w, жёсткость равна a. Потенциальная энергия равна П=aх²/2

ускорение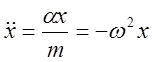

Полная энергия

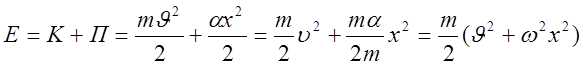
Среднее значение энергии получится после усреднения по Больцману.

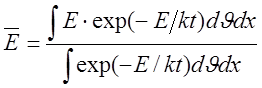          (2)

взяв в(2) интеграл, получим

        (3)

Это значит, что на каждую колебательную степень свободы приходится энергия =kt. Этот факт называется законом равнораспределения.

Если решётка состоит из N-атомов, то она имеет 3N степенней свободы, 3 из которых соответствут поступательному движению её как целой, и 3 вращательному . поэтому колебательных степеней свободы получается 3N-6. Однако, учитывая, что N очень велико » 10²³, то можно считать , что колебательных степенней свободы 3N. Тогда полная энергия решётки и её теплоёмкость равны

    ;             (4)

Последнее соотношение известно как закон Дюлота и Пти. (для одного моля).