Динамика решётки. Колебания одномерной одноатомной цепочки. Теплоёмкость твёрдых тел. Модель Эйнштейна, страница 4

 Если молекулы решётки состоят из нескольких атомов , то её теплоёмкость равна сумме теплоёмкостей, если бы она состояла из состовляющих атомов (правило Неймана-Реньо).

Теплоёмкость твёрдых тел.

Модель Эйнштейна.

Классическое выражение для теплоёмкости прямо согласуется с экспериментом только при достаточно высоких температурах. При низких же ,когда становятся существенными квантовые эффекты (длина волны Де-Бойля теплового движения атомов сравнима с расстоянием между ними).классическое рассмотрение не правомерно. Теплоёмкость в этих условиях зависит от температуры уменьшаясь одновременно с последней.

Первой попыткой уменьшения объяснения этого была предложена Эйнштейном теория относительности. Он считал что твёрдое тело представляет собой совокупность гармонических осцилляторов, колеблющихся с одной частотой (эйнштейновской ) w_Е Энергия без учёта нулевой.

          (1)

относительная вероятность для осциллятора находится в состоянии с энергией e равна (по Больцману)

 

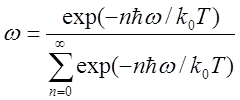
обозначим  х=е^-w/kt ,тогда

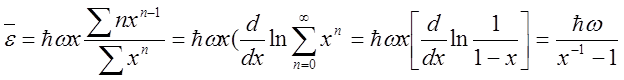        (3)

здесь использовано выражение для суммы геом.              S_n=b₁(qⁿ –1)/(q-1). Тогда средняя энергия осциллятора.

            (4)

Энергия моля вещества

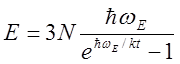              (5)

Найдём С, дифференцируя (5) по Т :

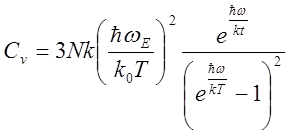
Обозначим Q_Е= - эйнштейновская температура тогда

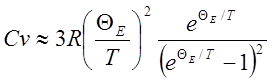       (6)

Q_Е порядка 300⁰ К, w_Е порядка 10¹³ Гц. Рассматривая (6) при Т>>Q_E и Т<<Q_E приходим, что в области высоких температур Сv=3R что согласуется с классической моделью. В области низких температур

   

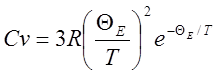
что не соответствует действительности. Т.о. модель Эйнштейна применима всегда, кроме слишком низких температур (Т<0,2Q_Е)

теплоёмкость твёрдых тел. Модель Дебоя

Тв. тело представляет собой совокупность 3N связанных гармонических осцилляторов . с разными частотами так, что средняя энергия осциллятора по-прежнему выражается как (4) и(9) . Ср – энергия  тв. тела:

               (1)

f – спектральная плотность. Нижний предел предположим равным нулю , для верхнего Дебай предположил существование максимальной частоты w_мах. А f(w) по аналогии с (5) и (7) предположил

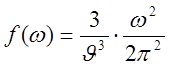     (2)

Здесь - определённым образом усредненная скорость звука. w_мах определяется из условия ,что полное число мод равно 3N.

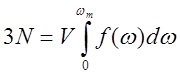          (3)

это даёт 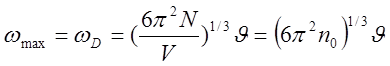       (4)

где n₀ – плотность атомов .

подставим (2) в (1):

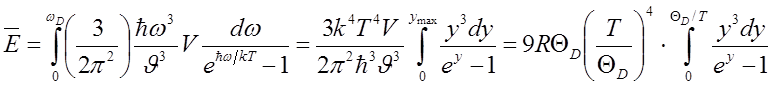    (5)

дифференцируем  (5) по Т

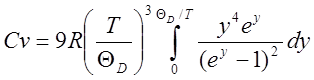      (6)

Последний интеграл не берущийся. Для него существуют таблицы. Однако можно вычислить теплоёмкость в предельных случаях низких и высоких температур. При высоких температурах получаем Сv=3R. При низких температурах верхний предел полагаем =¥

Тогда

 

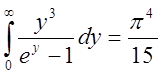
и

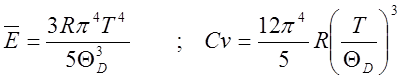          (7)

Эта зависимость соответствует экспериментальной. Определяя Q_D при некоторой Т, можно построить всю кривую. Однако ,Q_Dвообще говоря, сама зависит от Т.               Q_D

рис.1. В табл. 1 приведены некоторые температуры Дебая

для некоторых веществ.                                                                         105

                                                                                                                  100

                                                                                                                             5        10        15       К⁰

Медь	ГЦК	3420К	Никель	ГЦК	427
Цинк	ГПУ	316	Свинец	ГЦК	102
Алюминий	ГЦК	423	Натрий	ОЦК	157

Формула(6) показывает ,что ход теплоёмкости для разных веществ одинаково зависит от Q_D/Т .этот факт носит название закона соответственных состояний . в металлах кроме решёточной теплоёмкости , есть также теплоёмкость , обусловленная электронным газом. Эту составляющую мы рассмотрим в следующем разделе , когда речь пойдёт о электронных свойствах (электронная теория металлов).