Динамика решётки. Колебания одномерной одноатомной цепочки. Теплоёмкость твёрдых тел. Модель Эйнштейна, страница 2

особенностью выражения (20) является наличие нулевой энергии = 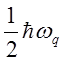 т.е. состояние покоя невозможно. Это согласуется с принципом неопределённости Гайзенберга. Число n_q называется главным квантовым числом. Видим что энергия  меняется на порции . Эти кванты энергии связываются с квазичастицами – фононами, число возбуждённых фононов с частотой w_q равно U_q. Фононы имеют спин = 0 и подчиняются статистике Бозе-Эйнштейна. Их число зависит от степени возбуждения системы. Следуя идеям Де-Бройля, мы здесь обращаем особое внимание на корпускулярный аспект колебаний решетке квазичастицы называют фононами с энергией  и квазиимпульсом   .

Колебания трёхмерного одноатомного кристалла.

В n 1 мы рассмотрели продольные колебания цепочки . можно также рассматривать продольные и поперечные колебания трёхмерного кристалла, но только для относительно симметричных структур и особых кристаллогр. направлений, которые соответствуют плоскостям атомов, движущихся синхронно. В куб. кристаллах волна может быть чисто продольной (L) или чисто поперечной (Т) в направлениях [100],[110] и [111]. Экспериментальные кривые приводятся для этих направлений. 

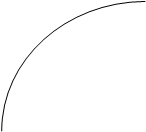
                                      Рис1

                                 

 

 

      000        q®      100                110       ¬q         000              000    q®     ½ ½ ½

На рис1 приведён пример дисперсионных кривых для меди (г ц к) в направлениях 100 к 110 поперечные моды совпадают. У других металлов такие кривые могут быть гораздо сложнее.

Спектры такого рода получают экспериментально, исследуя неупругое рассеивание тепловых нейтронов. Здесь используются законы сохранения энергии и квазиимпульса. При этом происходит уничтожение или   фонона.

         (1)

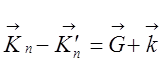            (2)

здесь Е и Е’ – энергии нейтрона до и после столкновения ,  - импульсы нейтрона, w - частота фонона,    - его вектор . в общем случае надо добавить в (2) вектор обр. решётки .

Эти исследования начались в 50-х годах и оказались весьма плодотворными.

Двухатомная линейная цепочка

Рассмотрим цепочку из атомов сорта А и В с массами m и М,       

равноудалённых друг от друга на расстояние а (рис.1)

Предположения относительна по справедливости закона Гука остаются в силе. Соседними атомами всегда будут атомы разных сортов. Сразу запишем ур-я движения :

                     

                (1)

снова имеем решения в виде волн. Однако из-за различных масс фазы и амплитуда волн будет различной      (2)

тогда

               (3)

Эта  система имеет решение для А и В, если детерминант =0.

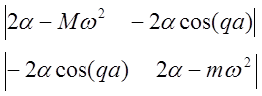 =0                 (4)

решая (4) получим

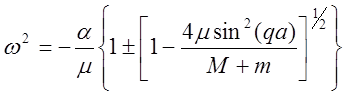              (5)

где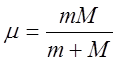 - приведённая масса , используя те же аргументы приходим к выводу, что разрешённые значения q даются выражением

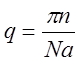       (6)

где N – число атомов одного сорта в цепочке. Все независимые решения находятся в интервале

        (7)

это есть зона Бриллюэна для решётки с параметром = 2а.

Из (5) видно, что одному q  соответствует два значения w.                                                       

При q®0

                                                                                                                                 

В первом случае                                                                 -п/2a                       0                     q   п/2a                                 

Во втором случае 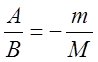                                                                              рис.1

Т.е. в нижней ветви атомы колеблются в фазе, а в верхней в противофазе. Нижнюю ветвь называют акустической модой, а верхнюю оптической. Первые возбуждаются в кристалле акустическим генератором, а вторые в щелочно-галоидных кристаллах электромагнитными волнами.

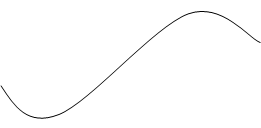  Более наглядно  видно различия между этими  

двумя типами колебаний при рассмотрении поперечных