Цель работы: измерение и расчет параметров колебательного контура.
Теоретические основы.
В цепи, содержащей индуктивность L, емкость С и активное сопротивление R могут возникать электрические колебания. Если зарядить конденсатор С от батареи Б до напряжения Uc (рис.1), а затем повернуть переключатель К вправо, то конденсатор начнет разряжаться через катушку и по цепи потечет электрический ток. Энергия электрического поля и напряжение на конденсаторе будут уменьшаться, но зато начнут возрастать энергия магнитного поля индуктивности и ток в цепи.
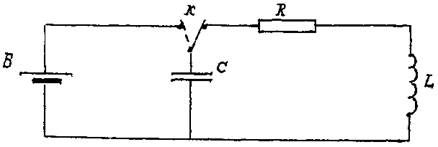 Когда напряжение на конденсаторе, а, следовательно, и
энергия электрического поля обратятся в нуль, энергия магнитного поля, а значит
и ток, достигнут наибольшего значения. Затем процесс протекает в обратном направлении:
ток и магнитная энергия катушки уменьшаются, а напряжение на конденсаторе и
энергия электрического поля возрастают. В дальнейшем процесс повторяется. В
цепи возникают колебания, называемые свободными, т.к. происходят без подвода
энергии извне, а сама электрическая цепь, содержащая элементы R, С, L, называется колебательным контуром.
Когда напряжение на конденсаторе, а, следовательно, и
энергия электрического поля обратятся в нуль, энергия магнитного поля, а значит
и ток, достигнут наибольшего значения. Затем процесс протекает в обратном направлении:
ток и магнитная энергия катушки уменьшаются, а напряжение на конденсаторе и
энергия электрического поля возрастают. В дальнейшем процесс повторяется. В
цепи возникают колебания, называемые свободными, т.к. происходят без подвода
энергии извне, а сама электрическая цепь, содержащая элементы R, С, L, называется колебательным контуром.
Согласно второму правилу Кирхгофа в любой момент времени сумма напряжений на элементах С и R контура равна ЭДС самоиндукции ES , возникающей в катушке L.
IR + UC = ES (2.1)
Из закона Фарадея ES = -L(dI/dt) следует
L(dI/dt) + IR + q/C = 0 (2.2)
Последнее уравнение можно записать в виде
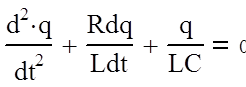
|
Здесь
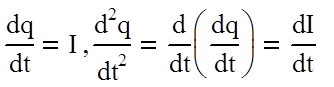
Введем следующие обозначения:
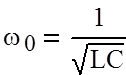 |
- циклическая частота собственных колебаний,
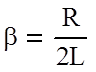 |
- коэффициент затухания,
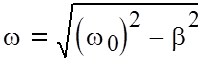 |
- циклическая частота затухающих колебаний.
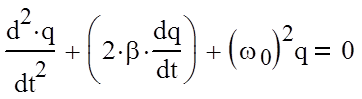 С учетом введенных обозначений дифференциальное
уравнение (2.3) запишем в виде
С учетом введенных обозначений дифференциальное
уравнение (2.3) запишем в виде
|
Последнее уравнение представляет собой уравнение затухающих электрических колебаний. Его решение имеет вид
q = q0l-btsin(wt + L) (2.5)
здесь L – начальная фаза колебаний.
Решение (2.5) получено при условии, что b2 < w02. В противном случае колебания не возникают, будет наблюдаться апериодический процесс разряда конденсатора. Разделив (2.5) на С, получим уравнение для напряжения на конденсаторе
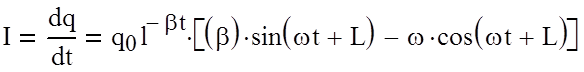 U = U0l-btsin(wt
+ L) (2.6)
U = U0l-btsin(wt
+ L) (2.6)
Продифференцировав (2.5) по времени получим уравнение для тока в контуре.
|
На рис.2 показана зависимость напряжения на конденсаторе от времени.
Период колебаний определяется по формуле
|
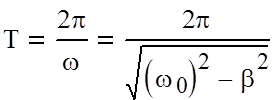
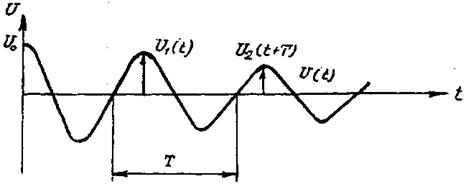
Важной характеристикой затухающих колебаний является логарифмический декремент.
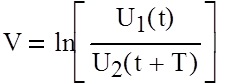 Логарифмический декремент V равен логарифму отношения двух последующих максимальных отклонений
напряжений в одну и ту же сторону
Логарифмический декремент V равен логарифму отношения двух последующих максимальных отклонений
напряжений в одну и ту же сторону
|
Из (2.6) следует, что U1(t) = U0l-bt; U2(t + T) = U0l-b(t+T)
и для логарифмического декремента можно записать
V = bt (2.10)
В ряде случаев удобно изучать колебательный процесс в системе координат I и U, называемой фазовой плоскостью. Кривая зависимости напряжения от тока на фазовой плоскости называется фазовой кривой.
Для идеального колебательного контура R = 0 имеем b = R/2L = 0
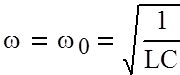
![]()
Отсюда
![]()
|
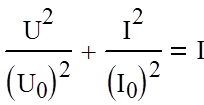 Система из двух уравнений (2.11) описывает
незатухающие колебания. Для получения уравнения фазовой кривой из (2.11) надо
исключить параметр t, получим
Система из двух уравнений (2.11) описывает
незатухающие колебания. Для получения уравнения фазовой кривой из (2.11) надо
исключить параметр t, получим
|
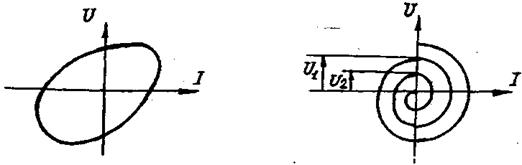 Это уравнение эллипса. Соответствующая (2.12) фазовая
кривая изображена на рис.3.
Это уравнение эллипса. Соответствующая (2.12) фазовая
кривая изображена на рис.3.
Рис.3 Рис.4
В реальном контуре, активное сопротивление которого отлично от нуля, колебания напряжения и тока описываются уравнениями (2.6) и (2.7). В этом случае амплитуды напряжения и тока в контуре монотонно убывают, и фазовая траектория получается незамкнутой (рис.4).
Метод измерений и описание установки.
На рис.5 показана принципиальная электрическая схема лабораторной работы.
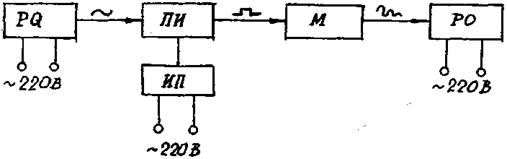
РО – осциллограф CI – 96
PQ – генератор импульсов ГЗ - 118
ПИ – преобразователь импульсов
М – модуль (колебательный контур)
ИП – источник питания «Марс».
Принципиальная схема модуля лабораторной работы М показана на рис.6.
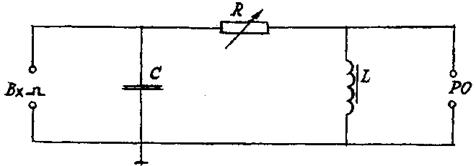
Рис.6.
Модуль содержит элементы колебательного контура: емкость С, катушку L, магазин сопротивлений R. Периодическая зарядка конденсатора С осуществляется через преобразователь импульсов ПИ в виде прямоугольных импульсов. Импульсы подаются на гнезда «Вх »
Затухающие колебания напряжения на конденсаторе наблюдаются на экране осциллографа РО при подключении его входа "Y" к соответствующим гнездам РО модуля М.
Общее сопротивление контура равно
Rобщ. = R + RK (3.1)
Где R – сопротивление магазина, RK – сопротивление катушки.
Параметры колебательного контура: индуктивность катушки L и емкость конденсатора С определяются с использованием графической зависимости V = f(R). Для различных величин сопротивлений магазина R определяются значения логарифмического декремента V.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.