Изучение вынужденных колебаний в колебательном контуре (Лабораторная работа № 25)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

ВОЛЖСКИЙ ФИЛИАЛ МОСКОВСКОГО ЭНЕРГЕТИЧЕСКОГО ИНСТИТУТА

(технический университет)

Кафедра механики и материаловедения

Лабораторная работа №25

Изучение вынужденных колебаний

в колебательном контуре

Выполнил: студент I курса

группы ТВТ – 02

Добрынин А.И.

Проверил: Мельников В.П.

Волжский 2003
Лабораторная работа №25

Изучение вынужденных колебаний

в колебательном контуре

1 Цель работы:

         Изучение резонансных кривых для силы тока.

2 Теоретические основы:

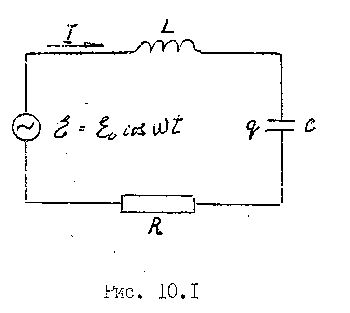
         В лабораторной работе изучаются вынужденные колебания, возникающие в колебательном контуре под воздействием внешней ЭДС, гармонически изменяющейся во времени t (рис. 10.1)  

         Зависимость амплитуды установившихся колебаний вблизи собственной частоты колебательного контура от частоты внешнего напряжения называют резонансной кривой.

         Рассмотрим процессы, протекающие в колебательном контуре, присоединенном к внешнему источнику, ЭДС которого изменяется по гармоническому закону:

         Обозначим через U напряжение на конденсаторе, а через I - ток в контуре.

         Согласно второму правилу Кирхгофа сумма напряжений на элементах цепи равна алгебраической сумме ЭДС в контуре:

                                                                   (1)

где 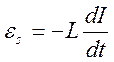- ЭДС самоиндукции, возникающей в катушке с индуктивностью L при прохождении в ней переменного тока.

         Уравнение (1) можно записать в виде:

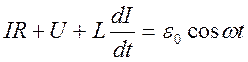                                                                 (2)

         Выразим напряжение в конденсаторе через ток:

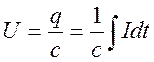
здесь q - заряд на конденсаторе. Подставляя в (2) найденное значение напряжения получим:

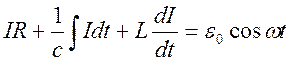
         Продифференцируем это выражение по t:

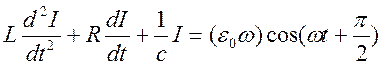                                                               (3)

         Далее будем использовать обозначения, введенные в лабораторной работе №6. Тогда (3) принимает вид:

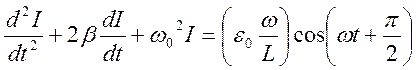                                                            (4)

         Полученное уравнение является линейным неоднородным (b = const,

w_о = const) дифференциальным уравнением второго порядка.

         Уравнения типа (4) описывают поведение широкого класса колебательных систем (электрических, механических и т.д.) под влиянием внешнего гармонического воздействия.

         Общее решение уравнения (4) равно сумме общего решения соответствующего однородного уравнения (без правой части) и частного решения неоднородного уравнения I = I₁ + I₂. Однородное уравнение

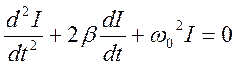
имеет решение . Затухание определяется множителем . За время

t = 1/b амплитуда колебаний уменьшится в e = 2,7… раз; при t >> 1/b слагаемое I₁ решения (4) стремится к нулю. Следовательно, слагаемое I₁ актуально для так называемого переходного процесса t £ 1/b.

         Установившиеся колебания в контуре, независимые от начальных условий, определяется частным решением уравнения I = I₂, которое имеет вид:

                                                                              (5)

здесь I_о - амплитудное значение силы тока;

          j - угол сдвига фаз между внешней ЭДС и током в цепи.

         Подставив (5) в (4), найдем значения I_о и j:

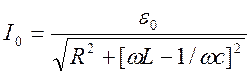                                                                         (6)

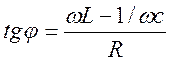                                                                                      (7)

         Из полученных результатов следует, что через некоторое время после включения гармонически изменяющейся ЭДС e = e_о coswt, t >> 1/b, которое потребуется для полного затухания собственных колебаний, в колебательном контуре устанавливается переменный ток с частотой, равной частоте вынуждающей ЭДС. При этом фазы вынуждающей ЭДС и возникающего в колебательном контуре тока сдвинуты на угол j.

         Из выражений (6) и (7) видно, что амплитуда тока и сдвиг фаз зависят от частоты w вынуждающей ЭДС. Анализ этих соотношений указывает на наличие экстремума функции I = f(w) при некоторой частоте w = w_рез. Эту частоту называют резонансной частотой:

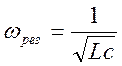                                                                             (8)