Цель работы: Изучение дифракции Фраунгофера на решетке, определение периода решетки и измерение длин волн спектра ртути.
Теоретические основы работы.
Дифракцией называется явление отклонения направления света от прямолинейности при распространении в среде с резко выраженными неоднородностями. Такими неоднородностями могут быть узкие щели, маленькие отверстия, тонкие препятствия. Размеры этих неоднородностей должны быть соизмеримы с длиной волны l.
В данной работе рассматривается дифракция света, вызываемая действием дифракционной решетки. Дифракционная решетка представляет собой совокупность большого числа одинаковых близко расположенных щелей. Расстояние d между серединами соседних щелей называется периодом решетки;
d = a + b
где а – ширина каждой щели;
b – ширина непрозрачного промежутка между щелями.
Если на такую решетку нормально падает монохроматическая волна, то на бесконечности или в фокальной плоскости линзы L (рис. 1) будет наблюдаться дифракционная картина с распределением интенсивности, представленным на рис. 2 (сплошная кривая). Пунктирной линией на рис. 2 показано распределение интенсивности в дифракционной картине от одной щели. На месте дифракционного максимума в картине от одной щели теперь наблюдается ряд интенсивных максимумов (главных) и дополнительных слабых максимумов (побочных). Между главными и побочными максимумами расположены побочные минимумы. При больном числе щелей побочные максимумы практически не видны.
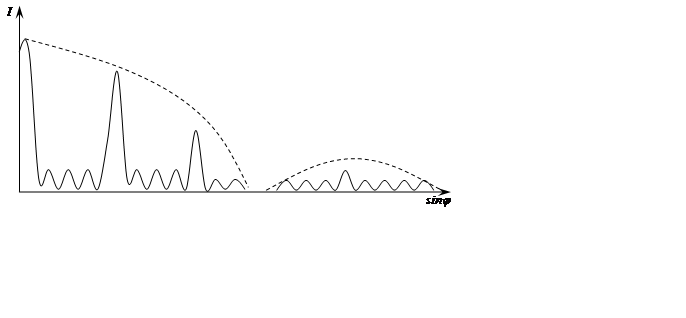
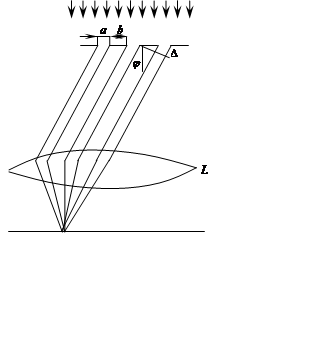
Рис. 1. Рис. 2.
Как видно из рис. 1, разность хода волн то двух соседних щелей ∆ = dsinj. Условие главных максимумов для дифракционной решетки выражается соотношением
![]() (1)
(1)
Число m в уравнении (1) называется порядком дифракционного максимума.
Если на решетку падает свет, содержащий ряд спектральных компонент, то в соответствии с формулой (1) главные максимумы для разных компонент образуются под разными углами: решетка разлагает свет в спектр. Характеристиками решетки для спектрального прибора являются угловая дисперсия и разрешающая способность.
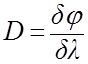 Дисперсия D
определяется как угловое расстояние между двумя спектральными линиями,
отличающимися по длинам волн на единицу, т.е.
Дисперсия D
определяется как угловое расстояние между двумя спектральными линиями,
отличающимися по длинам волн на единицу, т.е.
Разрешающей способностью называется величина
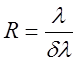 |
где dl - минимальный интервал длин волн, при котором две линии с длинами волн l и l+dl ещё разрешимы, т.е. видны раздельно. По критерию Ралея две близкие линии считаются ещё разрешимыми (видны раздельно), если главный максимум одной из них совпадает с минимумом (ближайшим к главному максимуму) другой (рис. 3).
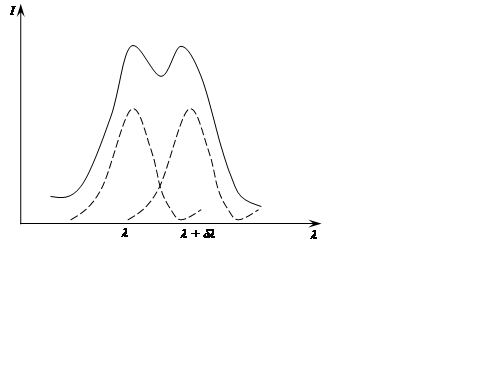 |
Рис. 3.
Описание метода и установки.
Оптическая схема установки представлена на рис. 4. Установка собирается на оптической скамье. Источником света является ртутная лампа 1. Параллельный пучок света, падающий на решетку 5, формируется линзами 2, 4 и щелью 3. Дифракционная картина наблюдается на экране 6 в виде спектральных линий синего, зеленого и желтого цвета. Эти линии отклоняются от оптической оси под различными углами j. Исходя из условия (1) можно определить длину волны, соответствующую видимой спектральной линии:
Период дифракционной решетки d определяется по формуле
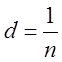 |
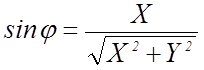 где n – число щелей в 1 мм решетки – величина постоянная
для каждой решетки.
где n – число щелей в 1 мм решетки – величина постоянная
для каждой решетки.
где Х – отклонение спектральной линии от оптической оси. Измеряется по шкале на экране.
Y – расстояние от решетки до экрана. Измеряется по линейке на оптической скамье.
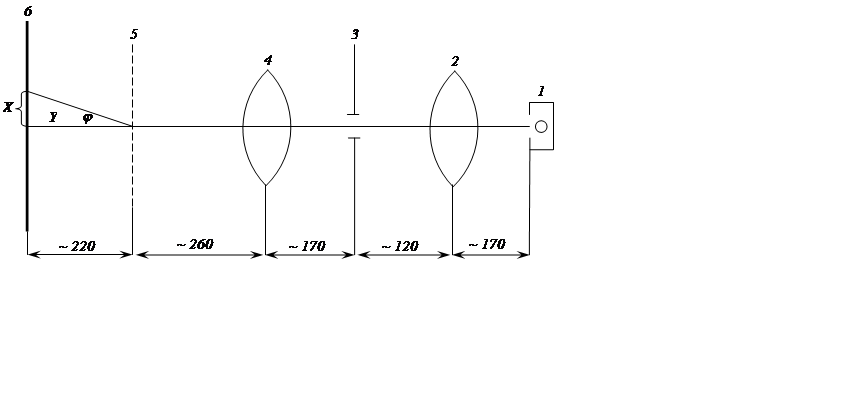 |
Рис. 4.
Порядок выполнения работы.
Все результаты занести в таблицу.
Данные для расчета и таблица результатов замера.
n = 580 – количество щелей в 1 мм решетки.
Цвет |
Х1, см |
Х2, см |
Хср, см |
Y, см |
sinj |
l, нм |
|
Синий |
6,1 |
6,1 |
6,1 |
22 |
0,267 |
460 |
|
Зеленый |
7,9 |
7,8 |
7,85 |
0,336 |
579 |
|
|
Желтый |
8,4 |
8,3 |
8,35 |
0,355 |
612 |
Обработка результатов замеров.
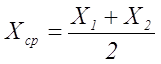 |
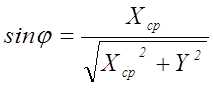 |
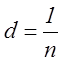 |
4. Определить длины волн для синей, зеленой и желтой линии спектра ртути.
Результат записать в таблицу в нанометрах.
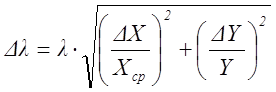 Рассчитать погрешность для одного из цветов (по
указанию преподавателя).
Рассчитать погрешность для одного из цветов (по
указанию преподавателя).где ∆Х = 0,5 мм – погрешность измерения по шкале экрана;
∆Y = 5 мм – погрешность измерения по линейке на оптической скамье.
Расчет.
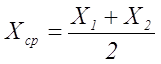 |
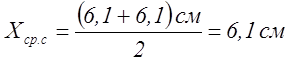
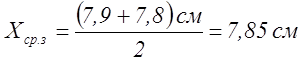
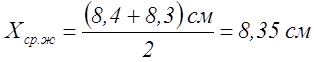
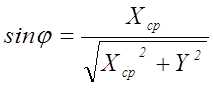 |
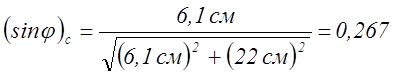
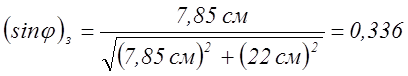
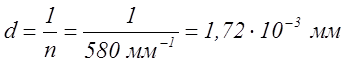 Определим период решетки:
Определим период решетки:4. Определим длины волн каждой линии спектра:
![]()
![]()
![]()
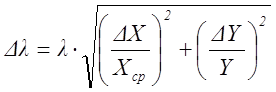 |
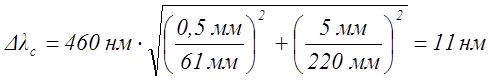
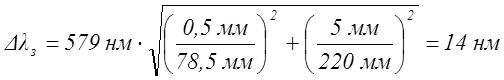
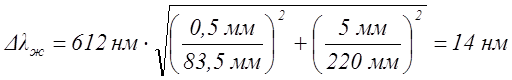
Контрольные вопросы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.