При этой частоте амплитуда тока достигает максимального значения (рис. 10.2)
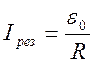 (9)
(9)
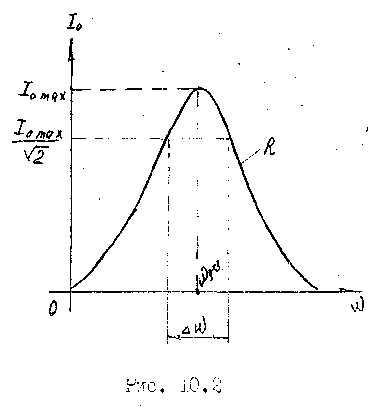
Итак, из (8) и (9) следует, что при w = wрез колебания силы тока достигают максимальной величины. Графическая зависимость амплитуды тока от частоты вынуждающей силы называется резонансной кривой. Чем меньше активное сопротивление контура, тем больше амплитуда силы тока при резонансе и ярче выраженная резонансная кривая.
Добротностью контура Q называют соотношение:
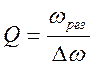 (10)
(10)
здесь Dw -
ширина резонансной кривой на высоте 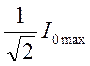
Из (10) следует, что чем «острее» резонансная кривая, тем больше добротность Q контура.
3. Метод измерений и описание установки
Принципиальная схема установки изображена на рис. 10.3:
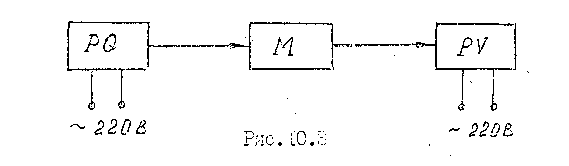
PQ - генератор импульсов ГЗ-118;
М - модуль (колебательный контур);
PV - вольтметр В7-38;
Электрическая схема модуля М показана на рис. 10.4:
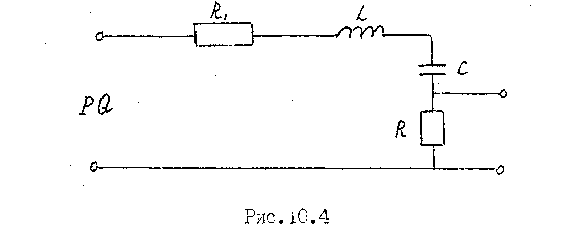
С выхода генератора звуковых сигналов (PQ) на вход модуля подается вынуждающая ЭДС, изменяющаяся по гармоническому закону.
Для снятия резонансной кривой Io = f(w) к гнездам PV модуля М подключается вольтметр. Измеряется напряжение Uо на сопротивлении R (ток I в контуре меняется синхронно с этим напряжением) при различных частотах n, задаваемых звуковым генератором.
|
n, Гц |
Uo, В |
w, рад/с |
Iо, А |
|
1000 |
0,012 |
6280 |
0,0012 |
|
1100 |
0,014 |
6908 |
0,0014 |
|
1200 |
0,017 |
7536 |
0,0017 |
|
1300 |
0,021 |
8164 |
0,0021 |
|
1400 |
0,027 |
8792 |
0,0027 |
|
1500 |
0,036 |
9420 |
0,0036 |
|
1600 |
0,053 |
10048 |
0,0053 |
|
1700 |
0,085 |
10676 |
0,0085 |
|
1800 |
0,126 |
11304 |
0,0126 |
|
1900 |
0,160 |
11932 |
0,0160 |
|
2000 |
0,077 |
12560 |
0,0077 |
|
2100 |
0,057 |
13188 |
0,0057 |
|
2200 |
0,047 |
13816 |
0,0047 |
|
2300 |
0,039 |
14444 |
0,0039 |
|
2400 |
0,034 |
15072 |
0,0034 |
|
2500 |
0,03 |
15700 |
0,003 |
1. Рассчитаем значения циклической частоты по формуле w = 2pn:
w1 = 2´3,14´1000 = 6280 рад/с
w2 = 2´3,14´1100 = 6908 рад/с
w3 = 2´3,14´1200 = 7536 рад/с
w4 = 2´3,14´1300 = 8164 рад/с
w5 = 2´3,14´1400 = 8792 рад/с
w6 = 2´3,14´1500 = 9420 рад/с
w7 = 2´3,14´1600 = 10048 рад/с
w8 = 2´3,14´1700 = 10676 рад/с
w9 = 2´3,14´1800 = 11304 рад/с
w10 = 2´3,14´1900 = 11932 рад/с
w11 = 2´3,14´2000 = 12560 рад/с
w12 = 2´3,14´2100 = 13188 рад/с
w13 = 2´3,14´2200 = 13816 рад/с
w14 = 2´3,14´2300 = 14444 рад/с
w15 = 2´3,14´2400 = 15072 рад/с
w16 = 2´3,14´2500 = 15700 рад/с
2. Рассчитаем значения амплитуд силы тока в контуре по формуле Io = Uo/R,
где R = 10 Ом:
Io1 = 0,012 / 10 = 0,0012 А
Io2 = 0,014 / 10 = 0,0014 А
Io3 = 0,017 / 10 = 0,0017 А
Io4 = 0,021 / 10 = 0,0021 А
Io5 = 0,027 / 10 = 0,0027 А
Io6 = 0,036 / 10 = 0,0036 А
Io7 = 0,053 / 10 = 0,0053 А
Io8 = 0,085 / 10 = 0,0085 А
Io9 = 0,126 / 10 = 0,0126 А
Io10 = 0,160 / 10 = 0,016 А
Io11 = 0,077 / 10 = 0,0077 А
Io12 = 0,057 / 10 = 0,0057 А
Io13 = 0,047 / 10 = 0,0047 А
Io14 = 0,039 / 10 = 0,0039 А
Io15 = 0,034 / 10 = 0,0034 А
Io16 = 0,03 / 10 = 0,003 А
3. Построим резонансную кривую Iо = f(w):
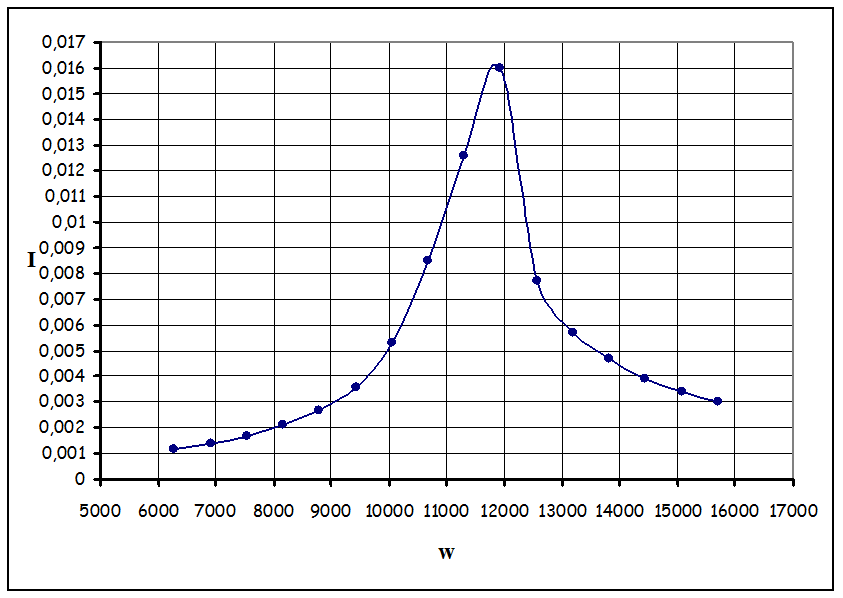
4. Определим добротность Q контура по формуле (10):
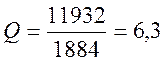
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.