Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление")

2.3   Алгоритмы текущей идентификации свойств объектов

В технических системах уравнение определения текущих значений критерия оптимальности, в реальном масштабе времени, имеет, как правило, нелинейный  вид.  Особенно популярным, в современных условиях, является  определение текущего значения критерия эффективности функционирования технической системы, который представляет собой технологический КПД, вычисляемый как отношение критерия управления измеренного техническими средствами автоматизации к критерию управления, прогнозируемому по эталонной математической модели:

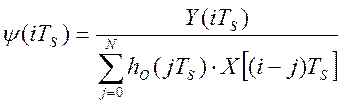
                   (2.27)

где N –длина массива, X(iT_S) – текущее значение управляющего воздействия; Y(iT_S) – текущее значение критерия оптимальности; h_O(jT_S) – эталонная динамическая модель технической системы. Критерий (2.27) относится к нелинейным с априорно известным максимумом. Поэтому решение задач синтеза информационно-измерительных подсистем для управляющих систем, работающих по таким критериям,  всегда требует линеаризации критерия оптимизации.  На рисунке 2.16 представлен макет виртуального прибора для  определения эффективности работы гидроагрегата [23] с помощью двух типовых модулей цифровой обработки информации.  На рисунке 2.20 представлена функциональная схема виртуального прибора [23], которая работает следующим образом. Текущие значения активной мощности гидроагрегата, Z₂(iT_S)   и   расхода воды через лопасти гидроагрегата, Z₁(iT_S)  измеряются с помощью типового алгоритмического модуля в ходе технологического процесса стандартными техническими средствами автоматизации. Результаты работы модуля ввода–вывода аналоговой информации  подаются на регистрацию, и вычисляется, с помощью эталонной математической модели, текущее значение эффективности функционирования гидроагрегата.

                 Z₁(iT_S)                                                         Z₂(iT_S)  

 

Рис. 5      Измерение эффективности работы гидроагрегата

Рис. 2.20  Прибор для измерения эффективности работы гидроагрегата [23]

Автоматизированное рабочее место оператора позволяет наблюдать за текущими изменениями активной мощности гидроагрегата, Z₂(iT_S),  текущими изменениями расхода воды, Z₁(iT_S)  и, главное, за текущими изменениями эффективности работы гидроагрегата: . При этом, эти тренды позволяют не только констатировать факт текущего состояния гидроагрегата, но и позволяют проводить как оптимизацию технологических режимов работы гидроагрегата, так и диагностику функционирования основного оборудования на предмет эффективности его функционирования. Это достигается основными алгоритмами идентификации текущих свойств технической системы.

2.3.1  Текущая идентификация положения рабочей точки

Метод наименьших квадратов имеет существенные преимущества перед другими методами: во-первых, он приводит к сравнительно простому алгоритму идентификации, а во-вторых, позволяет дать алгоритму идентификации теоретическое обоснование с вероятностной точки зрения. Постановка задачи выглядит следующим образом:

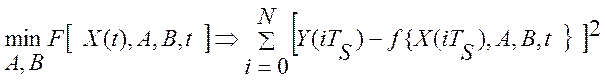                                      (2.28)

где - цифровая последовательность измеренных значений управляющего воздействия,  - цифровая последовательность измеренных значений критерия оптимальности,  - математическая модель технической системы. Так как в окрестности рабочей точки статическая характеристика технической системы, обычно линеаризуема в малом диапазоне изменения управляющего воздействия, то аппроксимирующая зависимость может быть выбрана прямой

.                                           (2.29)

Алгоритм идентификации вытекает из (2.28) путем дифференцирования и приравнивания к нулю первых производных по идентифицируемым параметрам. Подстановка (2.29) в (2.28) и дифференцирование по А и В дает:

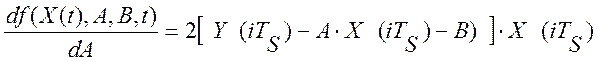
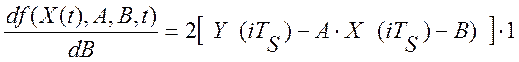
Приравнивание к нулю, полученных производных, дает систему алгебраических уравнений:

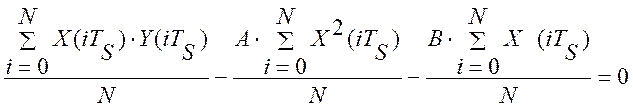
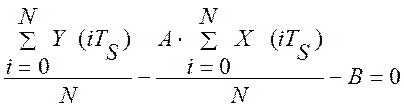                                                (2. 30)

Если использовать центрированные значения экспериментальных данных: , а , то все оценки нечетных начальных моментов в системе уравнений (2.30) преобразуются в нечетные центральные моменты и становятся равными нулю. Поэтому решением системы уравнений (2.30) является количественная оценка величины производной на периоде принятия решения (период управления) T_У=N_·T_S :

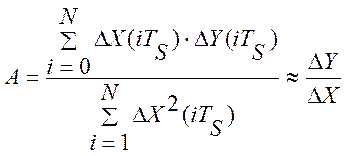,                                             (2.31)

где  ,  – текущие центрированные значения входного и выходного параметров объекта управления.

Коэффициент А есть не что иное как величина производной в рабочей точке при условии, что . Кроме того, в условиях нормального функционирования  есть не что иное как флуктуация управляющего воздействия, , вокруг своего математического ожидания  на периоде идентификации, T_И=T_У.

Поэтому выражение (2.31) представляет собой алгоритм вычисления величины производной (в одномерном случае) или составляющих градиента (в многомерном случае) по данным нормального функционирования и, следовательно, алгоритм статической идентификации положения рабочей точки (см. рисунок 2.21 и [1, 2]) может быть сформулирован следующим образом :