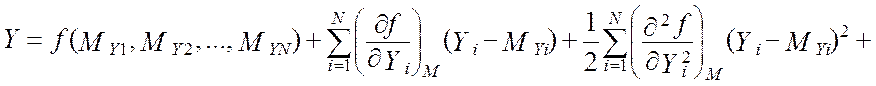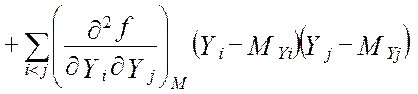Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 7

                                                                                                                   (2.35)

Применяя к  выражению (2.35) операцию взятия математического  ожидания, имеем:

         

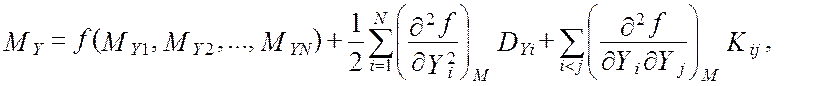где  K_{i j}  -  корреляционный момент величин Y_i , Y_j. Рассматривая случай, когда величины Y_i и Y_j  некоррелированы между собой, за ошибку линеаризации можно принять второе слагаемое формулы (2.35).  Однако, приняв во внимание вид линеаризуемой функции, можно утверждать, что линеаризация не изменяет математического ожидания функции. Действительно, для функции Y = Y₁Y₂ … Y_N  вторая частная производная по любому из аргументов равна нулю, а следовательно, в нуль будет обращаться и второе слагаемое формулы (2.35).

          Влияние рассматриваемого метода линеаризации на дисперсию случайной величины Y, можно проследить [20, 34], для случая некоррелированных случайных величин X₁ , X₂ ,…, X_N по модели дисперсии случайной функции, Y:

                                                                                                                        

Здесь, два последних слагаемых представляют собой поправку на нелинейность функции. Для исследуемой функции Y(Y₁,Y₂,...,Y_N)=Y₁Y₂...Y_N, второе слагаемое обращается в ноль. Таким образом, рассчитав значение третьего слагаемого в выражении (2.36), мы получим погрешность по дисперсии, вносимую при линеаризации функции разложением в ряд Тейлора.

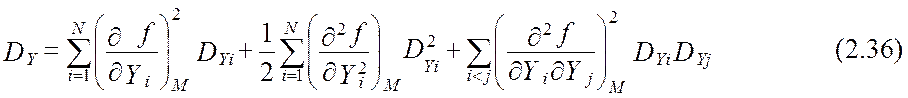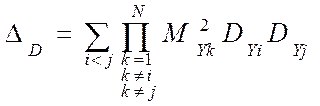          Однако оценивать  величину погрешности линеаризации, которая при таком подходе становится методической составляющей систематической погрешности  измерений, удобнее не по величине D_D , а по относительной погрешности линеаризации, которая позволяет соотнести величину погрешности линеаризации по дисперсии с величиной дисперсии случайной величины Y .

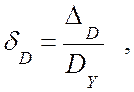
Итак, погрешность линеаризации уменьшается с уменьшением границ изменения аргументов линеаризуемой функции, которые однозначно определяются дисперсией перемножаемых сигналов.  Чем меньше отношение среднеквадратичного отклонения сигнала к его математическому ожиданию, тем меньше становится относительная погрешность линеаризации. Анализ промышленных сигналов в условиях установившихся режимов технологических процессов показал [6, 8, 9, 11, 12, 24, 27, ], что они характеризуются небольшими колебаниями относительно математического ожидания (не более 10 %), что позволяет применить полученные математические модели, основанные на линеаризации методом разложения в ряд Тейлора, на практике.

Рассматриваемый метод линеаризации использует величину Y как функцию нескольких случайных величин Y₁, Y₂, …, Y_N, однако на практике измеряемые величины изменяются в реальном масштабе времени и потому представляют собой случайные функции, что отражено в  уравнении измерения критерия управления. Возникает вопрос о допустимости линеаризации случайной функции Y(t) разложением в ряд Тейлора, то есть о возможности перехода в предшествующих выражениях от характеристик случайной величины M_Yi, D_Yi  к характеристикам случайной функции M_Yi(t), D_Yi(t). Учитывая, что обобщенный критерий управления является статической характеристикой объекта управления, то есть показания виртуального прибора зависят только от мгновенных значений измеряемых величин и не зависят от их значений в предшествующие или последующие моменты времени, а также принимая во внимание тот факт, что сечение случайной функции в некоторый момент времени t представляет собой обычную случайную величину, линеаризацию любой нелинейной функции методом разложения в ряд Тейлора, следует признать возможной, так как мы имеем дело со стационарными эргодическими цифровыми последовательностями. То есть, оценки статистических характеристик по множеству реализаций случайного процесса можно заменить оценками статистических характеристик, вычисленными по длине одной реализации.