Алгоритмы текущей идентификации свойств объектов (Раздел 2.3 учебника "Планово-экономическое управление"), страница 2

– накапливаются экспериментальные данные по входу, , и по выходу, , по которым оцениваются величины математических ожиданий по входу  и по выходу  (блоки 2, 3) и производится центрирование (блоки 4, 5);

– вычисляется величина производной  или величины составляющих градиента по всем направлениям (блоки 6, 7, 9);

– делается шаг в сторону достижения минимального значения критерия оптимизации (блоки 8, 10, 11).

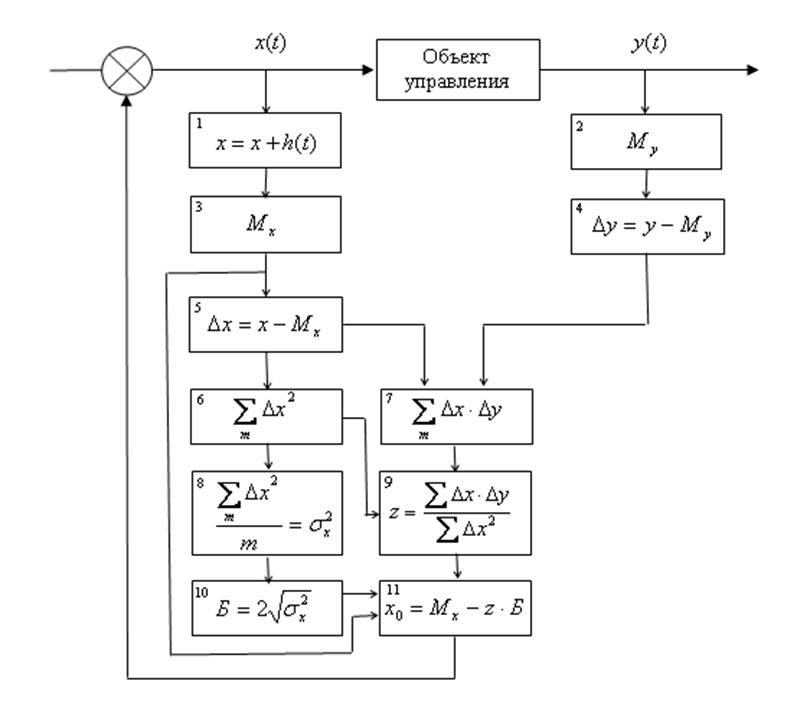
Рис. 2.21 – Блок-схема алгоритма идентификации текущего положения рабочей точки технической системы [1, 2]

Движение в сторону достижения экстремума осуществляется по выражению

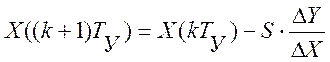,                                         (2.32)

где  ,  – текущее и предыдущее значения управляющего воздействия на k-том интервале идентификации; S- настроечный коэффициент (обычно );  - количественная оценка величины и знака производной в рабочей точке на статической характеристике технической системы.

Алгоритм позволяет отслеживать дрейф критерия оптимальности и следить за его перемещениями в реальном масштабе времени. Однако данный алгоритм не позволяет точно попасть в оптимум, а только следит за его перемещением. По знаку градиента можно принимать решение о направлении изменения управляющих координат при случайных перемещениях статической характеристики в пространстве управляющих координат. Составляющие вектора градиента могут являться рекомендациями по изменению управляющих воздействий при адаптивном управлении и, позволяют следить за перемещениями статической характеристики технической системы в пространстве управляющих координат.

Основным режимным параметром функционирования алгоритма является объем информации (), накапливаемой для обеспечения расчетов по соотношению (2.31, см. рис. 2.22) и оптимальная скважность всех решётчатых функции (цифровых последовательностей), T_S⁰ , используемых при вычислениях.

 

Рис.2.22.  К понятию оптимальной скважности цифровой последовательности 

Точность вычислений по формуле (2.31) возрастает при увеличении объема накопления и потери от ошибок идентификации (см. рис 2.22) уменьшаются. Поэтому предпочтительно большое количество измерений. Однако, чем больше измерений, тем дольше происходит накопление информации, тем дальше оптимальный режим «уплывает» и тем больше возрастают потери от скорости дрейфа (см. рис. 2.22). Поэтому существует компромисс между потерями от ошибок идентификации и потерями от скорости дрейфа статической характеристики технической системы. Разрешение данного компромисса – это  оптимальная скважность всех решётчатых функции, T_S⁰  (см. рис.2.22), которая обеспечивает оптимальный режим формирования всех цифровых последовательностей технической системы.

Применение рассматриваемого алгоритма особенно выгодно в условиях больших (по амплитуде) изменений входных параметров для малоинерционных и безынерционных объектов, характеристики которых подвержены медленному дрейфу.      Достоверность показаний виртуального прибора для оценки величины производной  зависят не столько от сложности объекта управления, сколько от точности и чувствительности применяемых технических средств измерения. При этом, на первый план выдвигается разработка алгоритмов визуализации процессов измерения и управления, а основной проблемой является количественно обоснованный выбор критерия эффективности работы энергооборудования.

Алгоритм позволяет отслеживать дрейф оптимального режима и наносить управляющее воздействие, компенсирующее этот дрейф. Однако данный алгоритм не позволяет точно попасть в оптимум, а только следит за его перемещением.

2.3.2 Текущая идентификация динамических свойств технической системы

Требования к математическим моделям динамических связей объекта идентификации, входящих в базу знаний  интеллектуальной измерительной системы должны быть идентичными требованиям к математическим моделям, перерабатываемых в технической системе,  сигналов,   как по форме, так и по содержанию. В пользу этого допущения говорит, хотя бы тот факт, что основным приемом идентификации динамических характеристик в интеллектуальных измерительных системах является решения уравнения свертки как основной модели динамического  объекта в задачах управления.